题目内容
17.下列有关命题的说法正确的是( )| A. | “若x≠a且x≠b,则x2-(a+b)x+ab≠0”的否命题为:“若x=a且x=b,则x2-(a+b)x+ab=0” | |
| B. | “x=-1”是“x2-5x-6=0”的根的逆命题是真命题 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
分析 一一判断即可得出结论.
解答 解:命题“若x≠a且x≠b,则x2-(a+b)x+ab≠0”的否命题是:若x=a或x=b,则x2-(a+b)x+ab=0,故A错误;
x=-1”是“x2-5x-6=0”的根的逆命题是:x2-5x-6=0的根是x=-1,是假命题,故B错误;
命题“?x∈R使x2+x+1<0”是特称命题,其否定命题为:?x∈R,使x2+x+1≥0,故C错误;
命题“若x=y,则sinx=siny”的逆否命题为命题“若sinx≠siny”,则“x≠y”,正确;
故选:D.
点评 判断逆命题、否命题、逆否命题的真假,有时可利用原命题与逆否命题同真同假,逆命题与否命题同真同假这一关系进行转化判断.当一个命题的真假不易判断时,往往可以转化为判断原命题的逆否命题的真假,因为它们是等价命题.另外,否命题和逆命题也是等价命题.

练习册系列答案
相关题目
8.若tanα=3,则tan(α-$\frac{π}{4}$)=( )
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
5.如图是一个程序框图,则输出的S的值是( )


| A. | -1 | B. | 0 | C. | 8 | D. | 9 |
12.设集合A={a,a2,-2},B={2,4},A∩B={4},则a=( )
| A. | 2 | B. | -2 | C. | 4 | D. | $\sqrt{2}$ |
9.设等差数列{an}的前n项和为Sn,且满足S2016>0,S2017<0,对任意正整数n,都有|an|≥|ak|,则k的值为( )
| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
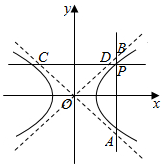 已知P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意一点,过P作x轴的垂线,分别交双曲线的两条渐近线于A,B两点,过P作y轴的垂线,分别交双曲线的两条渐近线于C,D两点.求证:|PA|•|PB|+|PC|•|PD|为定值.
已知P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意一点,过P作x轴的垂线,分别交双曲线的两条渐近线于A,B两点,过P作y轴的垂线,分别交双曲线的两条渐近线于C,D两点.求证:|PA|•|PB|+|PC|•|PD|为定值.