ƒøƒ⁄»ð
6£Æƒ≥π˙º ŒÔ¡˜”–œÞπ´ÀæÀ˘ ÙŒ£œ’∆∑≤÷ø‚∑¢…˙Ãÿ¥Û±¨’®£¨ƒ≥µÿ«¯—°≥ˆ600√˚œ˚∑¿πŸ±¯≤Œ”Α÷«¯æ»‘Æ£¨…Ë∆‰±ý∫≈Œ™001£¨002£¨°≠£¨600£¨Œ™¥ÚÕ®…˙√¸Õ®µ¿£¨œ»≤…”√œµÕ≥≥È—˘∑Ω∑®≥È≥ˆ50√˚Œ™œ»«≤≤ø∂”£¨«“Àʪ˙≥ȵ√µƒ“ª∏ˆ∫≈¬ÎŒ™003£¨’‚600√˚πŸ±¯¿¥‘¥”⁄≤ªÕ¨µƒœÿ –£¨¥”001µΩ300¿¥◊‘A –£¨¥”301µΩ495¿¥◊‘B –£¨¥”496µΩ600¿¥◊‘C –£¨‘Ú»˝∏ˆ –±ª≥È÷–µƒ»À ˝“¿¥ŒŒ™£®°°°°£©| A£Æ | 26£¨16£¨8 | B£Æ | 25£¨17£¨8 | C£Æ | 25£¨16£¨9 | D£Æ | 24£¨17£¨9 |
∑÷Œˆ ∏˘æðœµÕ≥≥È—˘µƒ∂®“«Û≥ˆ∫≈¬Îº‰∏Ùº¥ø…µ√µΩΩ·¬€£Æ
Ω‚¥ Ω‚£∫∫≈¬Îº‰∏ÙŒ™600°¬50=12£¨
‘ÚÀʪ˙≥ȵƒ∫≈¬ÎŒ™003£¨
‘Úππ≥…“ª∏ˆµ»≤Ó ˝¡–£¨Õ®œÓπ´ ΩŒ™3+12£®n-1£©=12n-9£¨
”…1°Ð12n-9°Ð300£¨º¥1°Ðn°Ð25£¨π≤”–25»À£¨
”…301°Ð12n-9°Ð495£¨º¥26°Ðn°Ð42£¨π≤”–17»À£¨
”…496°Ð12n-9°Ð600£¨º¥43°Ðn°Ð50£¨π≤”–8»À£¨
π »˝∏ˆ –±ª≥È÷–µƒ»À ˝“¿¥ŒŒ™25£¨17£¨8£¨
π —°£∫B£Æ
µ„∆¿ ±æÂ÷˜“™øº≤ÈœµÕ≥≥È—˘µƒ”¶”√£¨«Û≥ˆ—˘±æº‰∏Ù£¨¿˚”√µ»≤Ó ˝¡–Ω¯––«ÛΩ‚ «Ω‚戱浃πÿº¸£Æ

¡∑œ∞≤·œµ¡–¥∞∏
 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
œýπÿƒø
16£Æ‘⁄°˜ABC÷–£¨»˝∏ˆƒ⁄Ω«A£¨B£¨Cµƒ∂‘±þ∑÷± «a£¨b°¢c£¨»Áπ˚a£∫b£∫c=1£∫1£∫$\sqrt{3}$£¨‘ÚA£∫B£∫C=£®°°°°£©
| A£Æ | 1£∫1£∫2 | B£Æ | 1£∫1£∫3 | C£Æ | 1£∫1£∫4 | D£Æ | 1£∫1£∫5 |
17£Æœ¬¡–”–πÿ√¸Ã‚µƒÀµ∑®’˝»∑µƒ «£®°°°°£©
| A£Æ | °∞»Ùx°Ÿa«“x°Ÿb£¨‘Úx2-£®a+b£©x+ab°Ÿ0°±µƒ∑Ò√¸Ã‚Œ™£∫°∞»Ùx=a«“x=b£¨‘Úx2-£®a+b£©x+ab=0°± | |
| B£Æ | °∞x=-1°± «°∞x2-5x-6=0°±µƒ∏˘µƒƒÊ√¸Ã‚ «’Ê√¸Ã‚ | |
| C£Æ | √¸Ã‚°∞?x° R£¨ πµ√x2+x+1£º0°±µƒ∑Ò∂® «£∫°∞?x° R£¨æ˘”–x2+x+1£º0°± | |
| D£Æ | √¸Ã‚°∞»Ùx=y£¨‘Úsinx=siny°±µƒƒÊ∑Ò√¸Ã‚Œ™’Ê√¸Ã‚ |
14£Æƒ≥—ß–£∏þ»˝ƒÍº∂”–—ß…˙500»À£¨∆‰÷–ƒ–…˙300»À£¨≈Æ…˙200»À£¨Œ™¡À—–æø—ß…˙µƒ ˝—ß≥…º® «∑ҔΖ‘±”–πÿ£¨œ÷≤…”√∑÷≤„≥È—˘µƒ∑Ω∑®£¨¥”÷–≥È»°¡À100√˚—ß…˙£¨œ»Õ≥º∆¡ÀÀ˚√«∆⁄÷–øº ‘µƒ ˝—ß∑÷ ˝£¨»ª∫Û∞¥–‘±∑÷Œ™ƒ–°¢≈Æ¡Ω◊È£¨‘ŸΩ´¡Ω◊È—ß…˙µƒ∑÷ ˝∑÷≥…5◊È£∫[100£¨110£©£¨[110£¨120£©£¨[120£¨130£©£¨[130£¨140£©£¨[140£¨150]∑÷±º”“‘Õ≥º∆£¨µ√µΩ»ÁÕºÀ˘ 浃∆µ¬ ∑÷≤º÷±∑ΩÕº£Æ
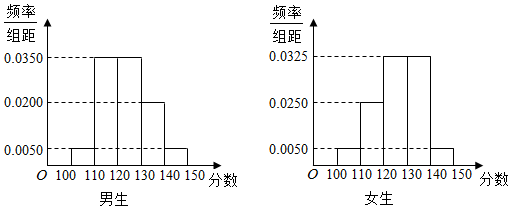
£®1£©¥”—˘±æ÷–∑÷ ˝–°”⁄110∑÷µƒ—ß…˙÷–Àʪ˙≥È»°2»À£¨«Û¡Ω»À«°∫√Œ™“ªƒ–“ª≈Ƶƒ∏≈¬ £ª
£®2£©»ÙπÊ∂®∑÷ ˝≤ª–°”⁄130∑÷µƒ—ß…˙Œ™°∞ ˝—ߺ‚◊”…˙°±£¨«Îƒ„∏˘æð“—÷™Ãıº˛ÕÍ≥…2°¡2¡–¡™±Ì£¨≤¢≈–∂œ «∑Ò”–90%µƒ∞—Œ’»œŒ™°∞ ˝—ߺ‚◊”…˙”Ζ‘±”–πÿ°±£ø
∏Ω£∫K2=$\frac{n£®ad-bc£©^{2}}{£®a+b£©£®c+d£©£®a+c£©£®b+d£©}$£Æ

£®1£©¥”—˘±æ÷–∑÷ ˝–°”⁄110∑÷µƒ—ß…˙÷–Àʪ˙≥È»°2»À£¨«Û¡Ω»À«°∫√Œ™“ªƒ–“ª≈Ƶƒ∏≈¬ £ª
£®2£©»ÙπÊ∂®∑÷ ˝≤ª–°”⁄130∑÷µƒ—ß…˙Œ™°∞ ˝—ߺ‚◊”…˙°±£¨«Îƒ„∏˘æð“—÷™Ãıº˛ÕÍ≥…2°¡2¡–¡™±Ì£¨≤¢≈–∂œ «∑Ò”–90%µƒ∞—Œ’»œŒ™°∞ ˝—ߺ‚◊”…˙”Ζ‘±”–πÿ°±£ø
| P£®K2°ðk0£© | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
1£Æ…˺Ø∫œP={1£¨2£¨3£¨4}£¨Q={x° R|0°Ðx°Ð3}£¨ƒ«√¥œ¬¡–Ω·¬€’˝»∑µƒ «£®°°°°£©
| A£Æ | P°…Q?Q | B£Æ | P°…Q?P | C£Æ | P°…Q=P | D£Æ | P°»Q=Q |
11£Æ»Ù µ ˝x£¨y¬˙◊„$\left\{\begin{array}{l}x+y-3°ð0\\ x-y-3°Ð0\\ 0°Ðy°Ð1\end{array}\right.$£¨‘Ú$z=\frac{2x+y}{x+y}$µƒ◊Ó–°÷µŒ™£®°°°°£©
| A£Æ | $\frac{5}{3}$ | B£Æ | 2 | C£Æ | $\frac{3}{5}$ | D£Æ | $\frac{1}{2}$ |
18£Æ…˵„P ««˙œþC£∫y=x3-$\sqrt{3}$x+$\frac{2}{3}$…œµƒ»Œ“‚“ªµ„£¨«˙œþC‘⁄Pµ„¥¶µƒ«–œþµƒ«„–±Ω«Œ™¶¡£¨‘ÚΩ«¶¡µƒ»°÷µ∑∂Œß «£®°°°°£©
| A£Æ | [$\frac{2}{3}$¶–£¨¶–£© | B£Æ | £®$\frac{¶–}{2}$£¨$\frac{5}{6}$¶–] | C£Æ | [0£¨$\frac{¶–}{2}$£©°»[$\frac{5}{6}$¶–£¨¶–£© | D£Æ | [0£¨$\frac{¶–}{2}$£©°»[$\frac{2}{3}$¶–£¨¶–£© |
15£Æ“—÷™∫Ø ˝f£®x£©µƒÕºœÛ‘⁄µ„£®x0£¨f£®x0£©£©¥¶µƒ«–œþ∑Ω≥Ãl£∫y=g£®x£©£¨»Ù∫Ø ˝f£®x£©¬˙◊„?x° l£®∆‰÷–IŒ™∫Ø ˝f£®x£©µƒ∂®“”ڣ©£¨µ±x°Ÿx0 ±£¨[f£®x£©-g£®x£©]£®x-x0£©£æ0∫„≥…¡¢£¨‘Ú≥∆x0Œ™∫Ø ˝f£®x£©µƒ°∞◊™’€µ„°±£¨»Ù∫Ø ˝f£®x£©=lnx-ax2-x‘⁄£®0£¨e]…œ¥Ê‘⁄“ª∏ˆ°∞◊™’€µ„°±£¨‘Úaµƒ»°÷µ∑∂ŒßŒ™£®°°°°£©
| A£Æ | $[{\frac{1}{{2{e^2}}}£¨+°Þ}£©$ | B£Æ | $£®{-1£¨\frac{1}{{2{e^2}}}}]$ | C£Æ | $[{-\frac{1}{{2{e^2}}}£¨1}£©$ | D£Æ | $£®{-°Þ£¨-\frac{1}{{2{e^2}}}}]$ |
16£Æ»Ùx£¨y¬˙◊„$\left\{\begin{array}{l}x°ð0\\ x+2y-3°ð0\\ 2x+y-3°Ð0\end{array}\right.$£¨‘Úu=2x+yµƒ◊Ó¥Û÷µŒ™£®°°°°£©
| A£Æ | 3 | B£Æ | $\frac{5}{2}$ | C£Æ | 2 | D£Æ | $\frac{3}{2}$ |