题目内容
已知某几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：几何体是直三棱柱消去一个三棱锥，结合直观图分别求出直三棱柱的体积和消去的三棱锥的体积，相减可得几何体的体积．
解答：
解：由三视图知：几何体是直三棱柱消去一个三棱锥，如图：
直三棱柱的体积为
×4×4×4=32．
消去的三棱锥的体积为
×
×2×4×4=
，
∴几何体的体积V=32-
=
，
故选：B
直三棱柱的体积为
| 1 |
| 2 |
消去的三棱锥的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 16 |
| 3 |
∴几何体的体积V=32-
| 16 |
| 3 |
| 80 |
| 3 |
故选：B
点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
已知函数f（x）=
，则f（x）的最小值为（ ）
|
| A、-4 | ||
| B、2 | ||
C、2
| ||
| D、4 |
某市司法部门为了宣传《宪法》举办法律知识问答活动，随机对该市18～68岁的人群抽取一个容量为n的样本，并将样本数据分成五组：[18，28），[28，38），[38，48），[48，58），[58，68），再将其按从左到右的顺序分别编号为第1组，第2组，…，第5组，绘制了样本的频率分布直方图；并对回答问题情况进行统计后，结果如下表所示．
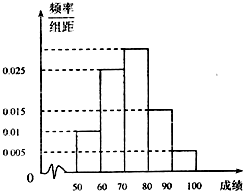国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”，方案要求以学校为单位组织实施，某校对高一1班同学按照“国家学生体质健康数据测试”项目按百分制进行了测试，并对50分以上的成绩进行统计，其频率分布直方图如图所示，若90～100分数段的人数为2人．