题目内容
(
+x2)3的展开式中的常数项为 .
| 1 |
| x |
考点:二项式系数的性质
专题:二项式定理
分析:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.
解答:
解:由于(
+x2)3的展开式的通项公式为 Tr+1=
•x3r-3,令3r-3=0,求得 r=1,
故(
+x2)3的展开式中的常数项为
=3,
故答案为:3.
| 1 |
| x |
| C | r 3 |
故(
| 1 |
| x |
| C | 1 3 |
故答案为:3.
点评:先求出二项式展开式的通项公式,再令x的幂指数等于0,求得r的值,即可求得展开式中的常数项的值.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知f(x)=
,则函数y=x•f(x)-1的零点个数为( )
|
|
| A、4 | B、3 | C、2 | D、1 |
已知点A(2,3),B(3,5),则直线AB的斜率为( )
| A、2 | B、-2 | C、1 | D、-1 |
下列函数是偶函数的是( )
| A、y=log2x |
| B、y=2x |
| C、y=cosx |
| D、y=x-1 |
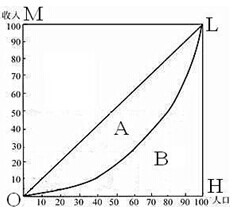 基尼系数是衡量一个国家贫富差距的标准.图中横轴OH表示人口(按收入由低到高分组)的累积百分比,纵轴OM表示收入的累积百分比,弧线OL(洛伦兹曲线)与对角线之间的面积A叫做“不平等面积”,折线段OHL与对角线之间的面积(A+B)叫做“完全不平等面积”,不平等面积与完全不平等面积之比等于基尼系数,则:
基尼系数是衡量一个国家贫富差距的标准.图中横轴OH表示人口(按收入由低到高分组)的累积百分比,纵轴OM表示收入的累积百分比,弧线OL(洛伦兹曲线)与对角线之间的面积A叫做“不平等面积”,折线段OHL与对角线之间的面积(A+B)叫做“完全不平等面积”,不平等面积与完全不平等面积之比等于基尼系数,则: