题目内容
已知集合A={x|x2+x-6≥0},B={x|x2-6x+5<0},C={x|m-1≤x≤2m}
(Ⅰ)求A∩B,(∁RA)∪B;
(Ⅱ)若B∩C=C,求实数m的取值范围.
(Ⅰ)求A∩B,(∁RA)∪B;
(Ⅱ)若B∩C=C,求实数m的取值范围.
考点:交、并、补集的混合运算,集合的包含关系判断及应用
专题:集合
分析:(Ⅰ)求出A与B中不等式的解集确定出A与B,求出A与B的交集,求出A补集与B的并集即可;
(Ⅱ)根据B与C的交集为C,得到C为B的子集,分C为空集与不为空集两种情况考虑,求出m的范围即可.
(Ⅱ)根据B与C的交集为C,得到C为B的子集,分C为空集与不为空集两种情况考虑,求出m的范围即可.
解答:
解:(Ⅰ)∵A={x|x≤-3或x≥2},B={x|1<x<5},
∴A∩B={x|2≤x<5},∁RA={x|-3<x<2},
则(∁RA)∪B={x|-3<x<5};
(Ⅱ)∵B∩C=C,∴C⊆B,
当C=∅时,则有m-1>2m,即m<-1;
当C≠∅时,则有
,
解得:2<m<
,
综上,m的取值范围是(-∞,-1)∪(2,
).
∴A∩B={x|2≤x<5},∁RA={x|-3<x<2},
则(∁RA)∪B={x|-3<x<5};
(Ⅱ)∵B∩C=C,∴C⊆B,
当C=∅时,则有m-1>2m,即m<-1;
当C≠∅时,则有
|
解得:2<m<
| 5 |
| 2 |
综上,m的取值范围是(-∞,-1)∪(2,
| 5 |
| 2 |
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
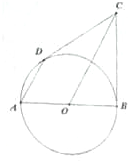 如图,AB为圆O的直径,BC与圆O相切于点B,D为圆O上的一点,AD∥OC,连接CD.
如图,AB为圆O的直径,BC与圆O相切于点B,D为圆O上的一点,AD∥OC,连接CD. 如图,直角△ABC所在平面外一点S,SA=SB=SC,点D为斜边AC的中点.
如图,直角△ABC所在平面外一点S,SA=SB=SC,点D为斜边AC的中点.