题目内容
圆x2+y2-2x+2y=0上的动点P到直线y=
x+2的距离的最小值为 .
| 3 |
| 4 |
考点:点到直线的距离公式
专题:直线与圆
分析:由圆的一般方程求出圆心坐标和半径,求出圆心到直线的距离,则答案可求.
解答:
解:由x2+y2-2x+2y=0,得(x-1)2+(y+1)2=2,
∴圆x2+y2-2x+2y=0的圆心为(1,-1),半径为
.
由y=
x+2,得3x-4y+8=0,
点(1,-1)到直线3x-4y+8=0的距离为
=3.
∴圆x2+y2-2x+2y=0上的动点P到直线y=
x+2的距离的最小值为3-
.
故答案为:3-
.
∴圆x2+y2-2x+2y=0的圆心为(1,-1),半径为
| 2 |
由y=
| 3 |
| 4 |
点(1,-1)到直线3x-4y+8=0的距离为
| |3×1-4×(-1)+8| | ||
|
∴圆x2+y2-2x+2y=0上的动点P到直线y=
| 3 |
| 4 |
| 2 |
故答案为:3-
| 2 |
点评:本题考查了圆的一般方程,考查了点到直线的距离公式,是基础题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
函数f(x)=2-x的大致图象为( )
A、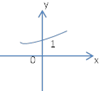 |
B、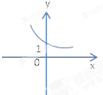 |
C、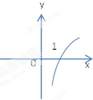 |
D、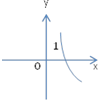 |
函数y=2-x的反函数的图象为( )
A、 |
B、 |
C、 |
D、 |
已知函数f(x)=sinx+acosx的图象关于直线x=
对称,且方程f(x)=m在[0,
)上恰有两个不同的实数根,则实数m取值范围是( )
| π |
| 6 |
| π |
| 2 |
| A、[0,1] | ||
| B、[1,2] | ||
C、[
| ||
D、[1,
|
已知集合A={x|x=2k-1,k∈Z},B={x|
≤0},则A∩B=( )
| x+1 |
| x-3 |
| A、[-1,3] |
| B、{-1,3} |
| C、{-1,1} |
| D、{-1,1,3} |