题目内容
17.下列说法正确的为④(只填序号).①若点P(a,2a)(a≠0)为角α终边上一点,则sinα=$\frac{2\sqrt{5}}{5}$;
②同时满足sinα=$\frac{1}{2}$,cosα=$\frac{\sqrt{3}}{2}$的角α有且只有一个;
③当|a|<1时,tan(arcsinα)的值恒正;
④方程tan(x+$\frac{π}{3}$)=$\sqrt{3}$的解集为{x|x=kπ,k∈Z}.
分析 ①根据三角函数的定义进行判断,
②根据三角函数的性质进行判断.
③根据反三角函数的性质进行判断,
④根据正切函数的性质进行求解判断即可.
解答 解:①若点P(a,2a)(a≠0)为角α终边上一点,则r=$\sqrt{{a}^{2}+4{a}^{2}}$=$\sqrt{5}$|a|,
则sinα=$\frac{2a}{\sqrt{5}|a|}$,若a>0,得sinα=$\frac{2a}{\sqrt{5}|a|}$=$\frac{2a}{\sqrt{5}a}$=$\frac{2\sqrt{5}}{5}$,
若a<0,则sinα=$\frac{2a}{\sqrt{5}|a|}$=-$\frac{2a}{\sqrt{5}a}$=-$\frac{2\sqrt{5}}{5}$,故①错误;
②同时满足sinα=$\frac{1}{2}$,cosα=$\frac{\sqrt{3}}{2}$的角α=2kπ+$\frac{π}{6}$,k∈Z,有无数多个,故②错误;
③当|a|<1时,arcsina∈(-$\frac{π}{2}$,$\frac{π}{2}$),所以tan(arcsina)∈R,故③错误,
④方程tan(x+$\frac{π}{3}$)=$\sqrt{3}$,则x+$\frac{π}{3}$=kπ+$\frac{π}{3}$,即x=kπ,即方程的解集为{x|x=kπ,k∈Z}.故②正确,
故答案为:④
点评 本题主要考查命题的真假判断,涉及三角函数的图象和性质,考查学生的推理和运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.4sin40°-tan40°的值为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}+\sqrt{3}}}{2}$ | D. | 2$\sqrt{2}$-1 |
8.实数a,b,则(a+b)(1+a)>0,是$\frac{1-b}{1+a}$<1恒成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.设集合A={x|x≥-1},B={x|y=ln(x-2)},则A∩(∁RB)=( )
| A. | [-1,+∞) | B. | [-1,2] | C. | [2,+∞) | D. | [-1,2) |
9.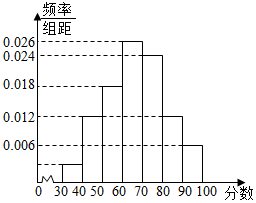 某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
(Ⅰ)估计该校高二年级学生在正式的数学学业水平考试中,成绩不合格的人数;
(Ⅱ) 请你根据已知条件将下列2×2列联表补充完整,并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”?
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$.
 某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.(Ⅰ)估计该校高二年级学生在正式的数学学业水平考试中,成绩不合格的人数;
(Ⅱ) 请你根据已知条件将下列2×2列联表补充完整,并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”?
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | a=12 | b= | |
| 女生 | c= | d=34 | |
| 合计 | n=100 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |
7.在等比数列{an}中,已知a2+a3=1,a3+a4=$\sqrt{2}$,则a14+a15等于( )
| A. | 16 | B. | 32 | C. | 64 | D. | 128 |