题目内容
用数学归纳法证明: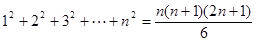
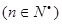
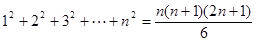
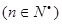
见解析
证明分两个步骤:一是先验证:当n=1时,等式成立;
二是先假设n=k时,原式成立。再证明当n=k+1时,等成也成立,再证明的过程中一定要用上n=k时的归纳假设
证明:⑴ 当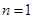 时,左边
时,左边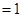 ,右边
,右边 ,即原式成立 ----4分
,即原式成立 ----4分
⑵ 假设当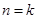 时,原式成立,即
时,原式成立,即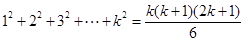 ----6分
----6分
当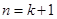 时,
时,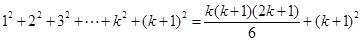
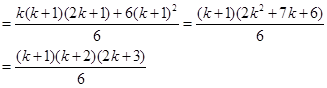
即当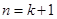 时原式也成立,由⑴⑵可知,对任意
时原式也成立,由⑴⑵可知,对任意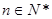 原等式都成立
原等式都成立
二是先假设n=k时,原式成立。再证明当n=k+1时,等成也成立,再证明的过程中一定要用上n=k时的归纳假设
证明:⑴ 当
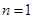 时,左边
时,左边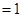 ,右边
,右边 ,即原式成立 ----4分
,即原式成立 ----4分⑵ 假设当
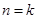 时,原式成立,即
时,原式成立,即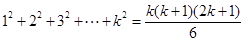 ----6分
----6分当
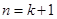 时,
时,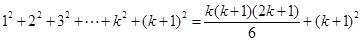
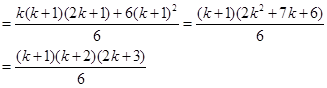
即当
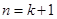 时原式也成立,由⑴⑵可知,对任意
时原式也成立,由⑴⑵可知,对任意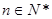 原等式都成立
原等式都成立
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 当
当 时,试猜想
时,试猜想 的值,并用数学归纳法给予证明。
的值,并用数学归纳法给予证明。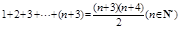 时,第一步验证
时,第一步验证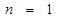 时,左边应取的项是
时,左边应取的项是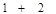
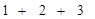
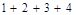
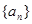 中,
中,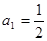 ,
,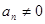 ,
, 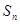 为该数列的前
为该数列的前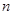 项和,且
项和,且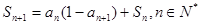 .
.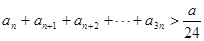 对一切正整数
对一切正整数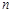 都成立,求正整数
都成立,求正整数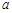 的最大值,并证明结论.
的最大值,并证明结论.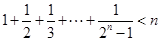 (
(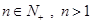 )时,第一步应验证的不等式是 .
)时,第一步应验证的不等式是 .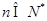 时,
时,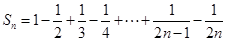 ,
,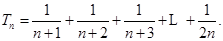
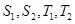 ;
;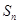 与
与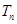 的关系,并用数学归纳法证明.
的关系,并用数学归纳法证明.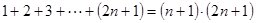 ”,在验证
”,在验证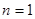 时,左边计算的值=___.
时,左边计算的值=___.