题目内容
(本小题满分14分)
已知数列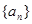 中,
中,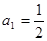 ,
,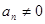 ,
, 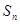 为该数列的前
为该数列的前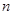 项和,且
项和,且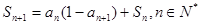 .
.
(1)求数列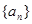 的通项公式;
的通项公式;
(2)若不等式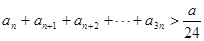 对一切正整数
对一切正整数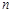 都成立,求正整数
都成立,求正整数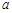 的最大值,并证明结论.
的最大值,并证明结论.
已知数列
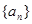 中,
中,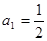 ,
,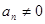 ,
, 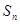 为该数列的前
为该数列的前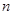 项和,且
项和,且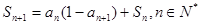 .
.(1)求数列
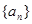 的通项公式;
的通项公式;(2)若不等式
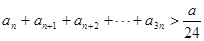 对一切正整数
对一切正整数 都成立,求正整数
都成立,求正整数 的最大值,并证明结论.
的最大值,并证明结论. (1)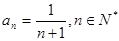 ;
;
(2).当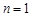 时,
时,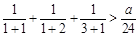 ,即
,即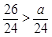 ,所以
,所以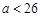 .而
.而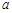 是正整数,所以取
是正整数,所以取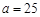 。
。
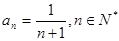 ;
;(2).当
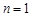 时,
时,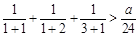 ,即
,即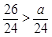 ,所以
,所以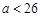 .而
.而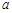 是正整数,所以取
是正整数,所以取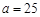 。
。本试题主要是考查了数列的通项公式的求解,和数列与不等式的综合运用。
(1)根据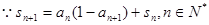 的,得到前n项和与通项公式的的关系,然后整体化简求解得到其通项公式的求解。
的,得到前n项和与通项公式的的关系,然后整体化简求解得到其通项公式的求解。
(2)不等式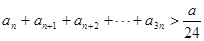 对一切正整数
对一切正整数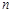 都成立,可以从特殊值入手,求解参数a的范围,然后分析得到结论。
都成立,可以从特殊值入手,求解参数a的范围,然后分析得到结论。
解:(1)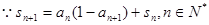
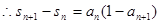
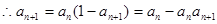 ………1分
………1分
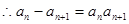 又
又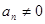
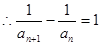 ………3分
………3分
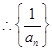 构成以2为首项,以1为公差的等差数列。
构成以2为首项,以1为公差的等差数列。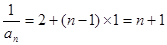
 ………6分
………6分
(2).当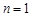 时,
时,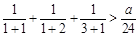 ,即
,即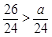 ,
,
所以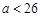 . ………7分
. ………7分
而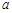 是正整数,所以取
是正整数,所以取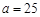 ,下面用数学归纳法证明:
,下面用数学归纳法证明: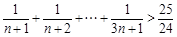 .
.
(1)当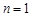 时,已证; ………8分
时,已证; ………8分
(2)假设当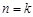 时,不等式成立,即
时,不等式成立,即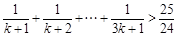 . ………9分
. ………9分
则当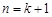 时,
时,
有
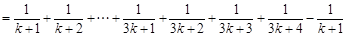
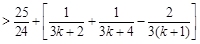 ………11分
………11分
因为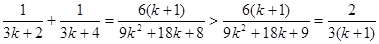
即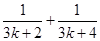 >
>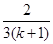 所以
所以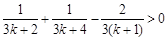 .
.
所以当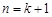 时不等式也成立.
时不等式也成立.
由(1)(2)知,对一切正整数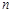 ,都有
,都有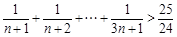 ,………13分
,………13分
所以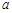 的最大值等于25. ………14分
的最大值等于25. ………14分
(1)根据
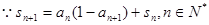 的,得到前n项和与通项公式的的关系,然后整体化简求解得到其通项公式的求解。
的,得到前n项和与通项公式的的关系,然后整体化简求解得到其通项公式的求解。(2)不等式
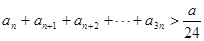 对一切正整数
对一切正整数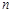 都成立,可以从特殊值入手,求解参数a的范围,然后分析得到结论。
都成立,可以从特殊值入手,求解参数a的范围,然后分析得到结论。解:(1)
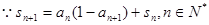
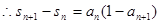
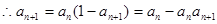 ………1分
………1分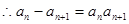 又
又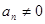
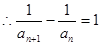 ………3分
………3分 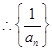 构成以2为首项,以1为公差的等差数列。
构成以2为首项,以1为公差的等差数列。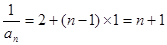
 ………6分
………6分(2).当
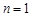 时,
时,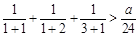 ,即
,即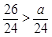 ,
, 所以
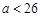 . ………7分
. ………7分而
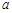 是正整数,所以取
是正整数,所以取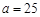 ,下面用数学归纳法证明:
,下面用数学归纳法证明: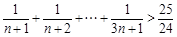 .
.(1)当
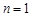 时,已证; ………8分
时,已证; ………8分(2)假设当
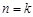 时,不等式成立,即
时,不等式成立,即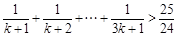 . ………9分
. ………9分则当
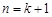 时,
时,有

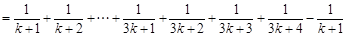
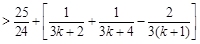 ………11分
………11分因为
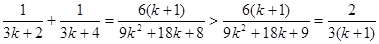
即
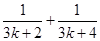 >
>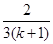 所以
所以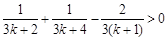 .
.所以当
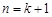 时不等式也成立.
时不等式也成立. 由(1)(2)知,对一切正整数
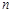 ,都有
,都有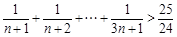 ,………13分
,………13分所以
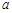 的最大值等于25. ………14分
的最大值等于25. ………14分
练习册系列答案
相关题目
 的各项均为正数,
的各项均为正数,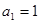 ,
,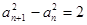
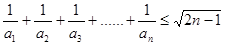 对一切
对一切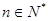 恒成立。
恒成立。 中,
中,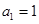 ,且
,且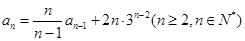 .
.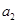 ,
,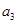 ,
,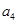 的值;
的值;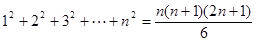
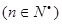
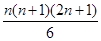
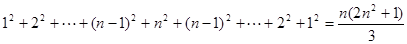 时,由
时,由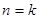 的假设到证明
的假设到证明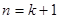 时,等式左边应添加的式子是( )
时,等式左边应添加的式子是( )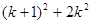
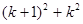
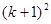
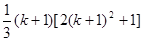
 时,在验证当
时,在验证当 时,等式左边为( )
时,等式左边为( )


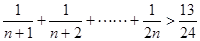 时,由k到k+1,不等式左端的变化是( )
时,由k到k+1,不等式左端的变化是( ) 项
项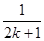 和
和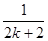 两项
两项 一项
一项