题目内容
已知定义在区间(0，＋∞)上的函数f(x)满足f(
)＝f(x1)－f(x2)，且当x>1时，f(x)>0.
(1)求f(1)的值，并判断f(x)的单调性；
(2)若f(4)＝2，求f(x)在[5,16]上的最大值．
(1)令x1＝x2>0，代入得f(1)＝f(x1)－f(x1)＝0，故f(1)＝0.
任取x1，x2∈(0，＋∞)，
且x1>x2，则>1，由于当x>1时，f(x)>0，
∴f()>0，即f(x1)－f(x2)>0，因此f(x1)>f(x2)，
∴函数f(x)在区间(0，＋∞)上是增加的．
(2)∵f(x)在(0，＋∞)上是增加的，
∴f(x)在[5,16]上的最大值为f(16)．
由f()＝f(x1)－f(x2)，
得f(
)＝f(16)－f(4)，
而f(4)＝2，∴f(16)＝4.
∴f(x)在[5,16]上的最大值为4.
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
，则f(f(3))＝( )
B．3
D.
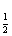x|的定义域是[a，b]，值域为[0,2]，对于区间[m，n]，称n－m为区间[m，n]的长度，则[a，b]长度的最小值为( )
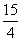B．3
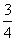
的值域为________．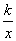
＋
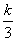在(1，＋∞)上是增函数，则实数k的取值范围是( )
若f(x0)≥2，则x0的取值范围是____________．
] B．[
＋y2＝1，若函数y＝f(x)的值域是(－1,1)，则f(x)一定是( )