题目内容
已知函数f(x)=x2-2x+k
(Ⅰ)若方程f(x)=1-x在(-∞,1]上有两个不等的实根,求实数k的取值范围;
(Ⅱ)是否存在实数k,当a+b≤2时,使得函数f(x)=x2-2x+k在定义域[a,b]上的值域恰为[a,b]?若存在,求出k的取值范围,若不存在,请说明理由.
(Ⅰ)若方程f(x)=1-x在(-∞,1]上有两个不等的实根,求实数k的取值范围;
(Ⅱ)是否存在实数k,当a+b≤2时,使得函数f(x)=x2-2x+k在定义域[a,b]上的值域恰为[a,b]?若存在,求出k的取值范围,若不存在,请说明理由.
考点:二次函数的性质,一元二次方程的根的分布与系数的关系
专题:函数的性质及应用
分析:(Ⅰ)化简得出x2-x+k=0,令g(x)=x2-x,(-∞,1],t(x)=1-k,运用图象求解即可.
(Ⅱ)假设存在实数k,当a+b≤2时,使函数f(x)在定义域[a,b]上的值域恰为[a,b],根据二次函数的单调性,建立方程关系即可得到结论
(Ⅱ)假设存在实数k,当a+b≤2时,使函数f(x)在定义域[a,b]上的值域恰为[a,b],根据二次函数的单调性,建立方程关系即可得到结论
解答:
解:(Ⅰ)∵f(x)=x2-2x+k,f(x)=1-x,
∴x2-2x+k=1-x,
即x2-x+k-1=0,
令g(x)=x2-x,(-∞,1],t(x)=1-k,
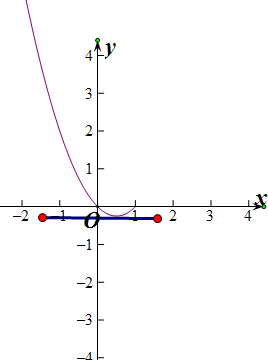
f(
)=-
,
根据图象可得出;-
<1-k≤0时,即1≤k<
,
方程f(x)=1-x在(-∞,1]上有两个不等的实根,
(Ⅱ)①若a<b≤1,在[a,b]上单调递减,
则
,①减②得:a+b=1,即b=1-a,
∴
,即
,
∴方程k-1-x-x2=0在x≤1上有两个不同的解,此时k∈[1,
)
②若a≤1≤b且1-a≥b-1,a+b≤2
在[a,b]上不单调时,
a=f(x)min=f(1)=k-1,b=k-2a+a2,b≤2-a
b=k-2a+a2≤a+1-2a+a2≤2-a,
∴a∈[-1,0],
∴k∈[0,1]
综上得:k∈[0,
).
∴x2-2x+k=1-x,
即x2-x+k-1=0,
令g(x)=x2-x,(-∞,1],t(x)=1-k,
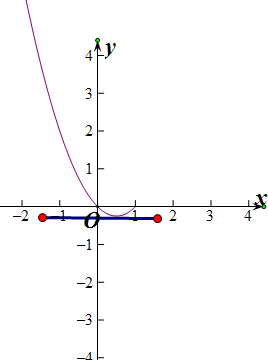
f(
| 1 |
| 2 |
| 1 |
| 4 |
根据图象可得出;-
| 1 |
| 4 |
| 5 |
| 4 |
方程f(x)=1-x在(-∞,1]上有两个不等的实根,
(Ⅱ)①若a<b≤1,在[a,b]上单调递减,
则
|
∴
|
|
∴方程k-1-x-x2=0在x≤1上有两个不同的解,此时k∈[1,
| 5 |
| 4 |
②若a≤1≤b且1-a≥b-1,a+b≤2
在[a,b]上不单调时,
a=f(x)min=f(1)=k-1,b=k-2a+a2,b≤2-a
b=k-2a+a2≤a+1-2a+a2≤2-a,
∴a∈[-1,0],
∴k∈[0,1]
综上得:k∈[0,
| 5 |
| 4 |
点评:本题考查方程根的存在问题,解题的关键是对于所给的函数式的分离参数,写出要求的参数转化为函数,再利用函数的图象解决.还考查函数与方程的综合运用,考查分类讨论的数学思想,考查学生分析解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设双曲线
-
=1(a>0,b>0)的离心率为
,且它的一个焦点与抛物线y2=24x的焦点重合,则此双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 某公司试销 一种新产品,规定试销时销售单 价不低于成本单价500元/件,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件),可近似看做一次函数y=kx+b的关系(图象如图所示).
某公司试销 一种新产品,规定试销时销售单 价不低于成本单价500元/件,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件),可近似看做一次函数y=kx+b的关系(图象如图所示).  如图,在平面直角坐标系xoy中,AO=8,AB=AC,sin∠ABC=
如图,在平面直角坐标系xoy中,AO=8,AB=AC,sin∠ABC=