题目内容
三个数0.89，90.8，log0.89的大小关系为（ ）
| A、0.89＜90.8＜log0.89 |
| B、log0.89＜0.89＜90.8 |
| C、log0.89＜90.8＜0.89 |
| D、0.89＜log0.89＜90.8 |
考点：对数值大小的比较,指数函数的图像与性质
专题：函数的性质及应用
分析：依据对数的性质，指数的性质，分别确定log0.89，0.89，90.8数值的大小，然后判定选项．
解答：
解：∵0.89∈（0，1）；90.8＞1；log0.89＜0
所以：log0.89＜0.89＜90.8
故选：B
所以：log0.89＜0.89＜90.8
故选：B
点评：本题考查对数值大小的比较，分数指数幂的运算，是基础题．
练习册系列答案
相关题目
若f（lgx）=x，则f（2）=（ ）
| A、lg2 |
| B、2 |
| C、102 |
| D、210 |
以下说法错误的是（ ）
| A、命题“若x2-3x+2=0，则x=1”的逆否命题是“若x≠1，则x2-3x+2≠0” |
| B、“x=1”是“x2-3x+2=0”的充分不必要条件 |
| C、若p∧q为假命题，则p，q均为假命题 |
| D、若命题p：?x0∈R，使得x02+x0+1＜0，则﹁p：?x∈R，都有x2+x+1≥0 |
三个数0.89，90.8，log0.89的大小关系为（ ）
| A、log0.89＜0.89＜90.8 |
| B、0.89＜90.8＜log0.89 |
| C、log0.89＜90.8＜0.89 |
| D、0.89＜log0.89＜90.8 |
已知集合A满足{1，2}⊆A⊆{1，2，3，4}，则集合A的个数为（ ）
| A、8 | B、2 | C、3 | D、4 |
已知集合A={x|x2+x-2＜0}，B={x|x＞0}，则集合A∩B等于（ ）
| A、{x|x＞-2} |
| B、{x|0＜x＜1} |
| C、{x|x＜1} |
| D、{x|-2＜x＜1} |
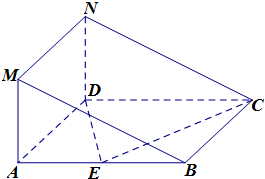如图所示的几何体中，四边形ABCD是菱形，ADNM是矩形，平面ADNM⊥平面ABCD，∠DAB=