题目内容
以下说法错误的是（ ）
| A、命题“若x2-3x+2=0，则x=1”的逆否命题是“若x≠1，则x2-3x+2≠0” |
| B、“x=1”是“x2-3x+2=0”的充分不必要条件 |
| C、若p∧q为假命题，则p，q均为假命题 |
| D、若命题p：?x0∈R，使得x02+x0+1＜0，则﹁p：?x∈R，都有x2+x+1≥0 |
考点：四种命题
专题：简易逻辑
分析：写出原命题的逆否命题，可判断A；根据充要条件的定义，可判断B；根据复合命题真假判断的真值表，可判断C；根据特称命题的否定方法，可判断D．
解答：
解：命题“若x2-3x+2=0，则x=1”的逆否命题是“若x≠1，则x2-3x+2≠0”，故A正确；
“x=1”时，“x2-3x+2=0”成立，故“x=1”是“x2-3x+2=0”的充分条件；
“x2-3x+2=0”时，“x=1或x=2”，即“x=1”不一定成立，故“x=1”是“x2-3x+2=0”的不必要条件，故B正确；
若p∧q为假命题，则p，q存在至少一个假命题，不一定全为假命题，故C错误；
命题p：?x0∈R，使得x02+x0+1＜0，则﹁p：?x∈R，都有x2+x+1≥0，故D正确；
故选：C
“x=1”时，“x2-3x+2=0”成立，故“x=1”是“x2-3x+2=0”的充分条件；
“x2-3x+2=0”时，“x=1或x=2”，即“x=1”不一定成立，故“x=1”是“x2-3x+2=0”的不必要条件，故B正确；
若p∧q为假命题，则p，q存在至少一个假命题，不一定全为假命题，故C错误；
命题p：?x0∈R，使得x02+x0+1＜0，则﹁p：?x∈R，都有x2+x+1≥0，故D正确；
故选：C
点评：本题考查的知识点是四种命题，充要条件，复合命题，特称命题，是简单逻辑的综合考查，难度不大，属于基础题．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
定义在R上的奇函数f（x），当x＞0时，f（x）=3；则奇函数f（x）的值域是（ ）
| A、（-∞，-3]∪[3，+∞） |
| B、（-∞，-3]∪[3，+∞）∪{0} |
| C、[-3，3] |
| D、{-3，0，3} |
设a=90.9，b=270.48，c=(
)-1.5，则a，b，c的大小顺序为（ ）
| 1 |
| 3 |
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞a＞c |
| D、c＞a＞b |
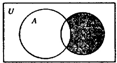设集合U={1，2，3，4，5}，A={1，2，3}，B={2，4}，则图中阴影部分所表示的集合是（ ）| A、{1，3，4} |
| B、{2，4} |
| C、{4，5} |
| D、{4} |
三个数0.89，90.8，log0.89的大小关系为（ ）
| A、0.89＜90.8＜log0.89 |
| B、log0.89＜0.89＜90.8 |
| C、log0.89＜90.8＜0.89 |
| D、0.89＜log0.89＜90.8 |