题目内容
8. 如图所示的封闭区域的边界是由两个关于x轴对称的半圆与截取于同一双曲线的两段曲线组合而成的,其中上半圆所在圆的方程是x2+y2-4y-4=0,双曲线的左右顶点A、B是该圆与x轴的交点,双曲线与该圆的另两个交点是该圆平行于x轴的一条直径的两个端点.
如图所示的封闭区域的边界是由两个关于x轴对称的半圆与截取于同一双曲线的两段曲线组合而成的,其中上半圆所在圆的方程是x2+y2-4y-4=0,双曲线的左右顶点A、B是该圆与x轴的交点,双曲线与该圆的另两个交点是该圆平行于x轴的一条直径的两个端点.(1)求双曲线的方程;
(2)记双曲线的左、右焦点为F1、F2,试在封闭区域的边界上求点P,使得∠F1PF2是直角.
分析 (1)根据上半个圆所在圆的方程得出两圆的圆心与半径,再求出双曲线的顶点坐标与标准方程;
(2)设点P的坐标,根据∠F1PF2是直角得出方程x2+y2=8,分别与双曲线和圆的方程联立,即可求出点P的坐标,注意检验,排除不合题意的坐标.
解答 解:(1)上半个圆所在圆的方程为x2+y2-4y-4=0,圆心为(0,2),半径为2$\sqrt{2}$;
则下半个圆所在圆的圆心为(0,-2),半径为2$\sqrt{2}$;
双曲线的左、右顶点A、B是该圆与x轴的交点,即为(-2,0),(2,0),即a=2,
由于双曲线与半圆相交于与x轴平行的直径的两端点,则令y=2,解得x=±2$\sqrt{2}$,
即有交点为(±2$\sqrt{2}$,2);
设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),
则$\frac{8}{{a}^{2}}$-$\frac{4}{{b}^{2}}$=1,且a=2,解得b=2;
所以双曲线的方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{4}$=1;
(2)双曲线的左、右焦点为F1(-2$\sqrt{2}$,0),F2(2$\sqrt{2}$,0),
若∠F1PF2是直角,设点P(x,y),则有x2+y2=8,
由$\left\{\begin{array}{l}{{x}^{2}{+y}^{2}=8}\\{{x}^{2}{-y}^{2}=4}\end{array}\right.$,
解得x2=6,y2=2;
由$\left\{\begin{array}{l}{{x}^{2}{+y}^{2}=8}\\{{x}^{2}{+(y±2)}^{2}=8}\end{array}\right.$,
解得y=±1(不满足题意,应舍去);
所以在封闭区域的边界上所求点P的坐标为(±$\sqrt{6}$,$\sqrt{2}$)和(±$\sqrt{6}$,-$\sqrt{2}$).
点评 本题考查了双曲线的标准方程的求法问题,也考查了圆与圆、圆与双曲线的位置关系,是综合性题目.

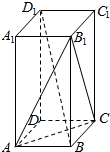
| A. | BD1∥B1C | B. | A1D1∥平面AB1C | C. | BD1⊥AC | D. | BD1⊥平面AB1C |
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{10}$ |
| A. | 当k≥0时,有1个零点;当k<0时,有2个零点 | |
| B. | 当k≥0时,没有零点;当-$\frac{1}{2}$<k≤-$\frac{1}{4}$时,有3个零点,当k≤-$\frac{1}{2}$或-$\frac{1}{4}$<k<0有2个零点 | |
| C. | 当k≥0时,没有零点;当-$\frac{1}{2}$<k<0时,有3个零点,当k≤-$\frac{1}{2}$有2个零点 | |
| D. | 当k≥0时,没有零点;当-$\frac{1}{2}$≤k<-$\frac{1}{4}$时,有3个零点,当k<-$\frac{1}{2}$或-$\frac{1}{4}$≤k<0有2个零点 |
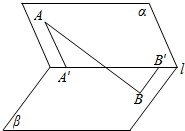 如图,二面角a-l-β为60°,A∈a,B∈β,AA′⊥l交l于A′,BB′⊥l交1于B′,若AA′=2,BB′=1,A′B′=$\sqrt{3}$.
如图,二面角a-l-β为60°,A∈a,B∈β,AA′⊥l交l于A′,BB′⊥l交1于B′,若AA′=2,BB′=1,A′B′=$\sqrt{3}$.