题目内容

7．某校食堂使用大小、手感完全一样的餐票，小明口袋里有一元餐票2张，两元餐票2张，五元餐票1张，若他从口袋中随意摸出2张，则其面值之和不少于四元的概率为（　　）
A．$\frac{3}{10}$B．$\frac{2}{5}$C．$\frac{1}{2}$D．$\frac{3}{5}$

分析 他从口袋中随意摸出2张，求出基本事件总数，再求出其面值之和不少于四元包含的基本事件个数，由此能求出其面值之和不少于四元的概率．

解答 解：小明口袋里有一元餐票2张，两元餐票2张，五元餐票1张，
若他从口袋中随意摸出2张，基本事件总数n=${C}_{5}^{2}$=10，
其面值之和不少于四元包含的基本事件个数m=${C}_{2}^{1}{C}_{1}^{1}+{C}_{2}^{1}{C}_{1}^{1}+{C}_{2}^{2}$=5，
∴其面值之和不少于四元的概率p=$\frac{m}{n}=\frac{5}{10}$=$\frac{1}{2}$．
故选：C．

点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．

练习册系列答案
相关题目
8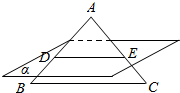．如图，已知△ABC是边长为2的正三角形，O是它的中心，过点O作BC平行的平面α，分别交AB，AC于点D，E，则四边形BCED的面积是（　　）
A．$\frac{5\sqrt{3}}{9}$B．$\frac{4\sqrt{3}}{9}$C．$\frac{\sqrt{3}}{3}$D．$\frac{2\sqrt{3}}{3}$
9．若复数z1=i3，z2=2+i，则z1z2=（　　）
A．-1-2iB．-1+2iC．1+2iD．1-2i
15．如图，建立平面直角坐标系xOy，x轴在地平面上，y轴垂直于地平面，单位长度为1千米，某炮位于坐标原点．已知炮弹发射后的轨迹在方程$y=kx-\frac{1}{20}（1+{k^2}）{x^2}（k＞0）$表示的曲线上，其中k与发射方向有关．炮的射程是指炮弹落地点的横坐标．
（1）当k=2时，求炮的射程；
（2）求炮的最大射程；
（3）设在第一象限有一飞行物（忽略其大小），其飞行高度为3.2千米，试问它的横坐标a不超过多少时，炮弹可以其中它？请说明理由．
2．以下四个命题中，其中真命题的个数为（　　）
①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
②对于命题p：?x∈R，使得x2+x+1＜0．则￢p：?x∈R，均有x2+x+1≥0；
③“x＜0”是“ln（x+1）＜0”的充分不必要条件；
④命题p：“x＞3”是“x＞5”的充分不必要条件．
A．1B．2C．3D．4
12．为评估设备M生产某种零件的性能，从设备M生产零件的流水线上随机抽取100件零件作为样本，测量其直径后，整理得到下表：
直径/mm5859616263646566676869707173合计
件数11356193318442121100
经计算，样本的平均值μ=65，标准差σ=2.2，以频率值作为概率的估计值．
（Ⅰ）为证判一台设备的性能，从该设备加工的零件中任意抽取一件，记其直径为X，并根据以下不等式进行评判（P表示相就事件睥概率）：①P（μ-σ＜X≤μ+σ）≥0.6826，②P（μ-2σ＜X≤μ+2σ）≥0.9544，③P（μ-3σ＜X≤μ+3σ）≥0.9974，评判规则为：若同时满足上述三个不等式，则设备等级为甲；若仅满足其中两个，则等级为乙，若仅满足其中一个，则等级为丙；若全部都不满足，则等级为丁，试判定设备M的性能等级．
（Ⅱ）将直径小于等于μ-2σ或直径不大于μ+2σ的零件认为是次品，从样本所含次品中任取2件，则它们的直径之差不超过1mm的概率是多少？
19．执行如图所示的程序框图（其中[x]表示不超过实数x的最大整数），则运行后输出的结果是（　　）
A．31B．33C．35D．37
16．已知函数$g（x）=\frac{x}{{{x^2}+ax+b}}$是奇函数，且满足g（1）=g（4）．
（1）求实数a，b的值；
（2）若$f（x）=\frac{1}{g（x）}（x≠0）$，当x∈[2，+∞）时，函数f（x）的图象上是否存在不同的两点，使过这两点的直线平行于x轴；
（3）对于（2）中的f（x），是否存在实数k同时满足以下两个条件：①不等式$f（x）+\frac{k}{2}＞0$对x∈[0，+∞）恒成立，②方程f（x）=k在x∈[-8，-1）上有解．若存在，求出实数k的取值范围；若不存在，请说明理由．
17．在△ABC中，a=2$\sqrt{3}$，c=2$\sqrt{2}$，A=60°，则C=（　　）
A．30°B．45°C．45°或135°D．60°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网