Question

8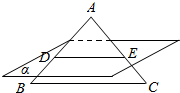．如图，已知△ABC是边长为2的正三角形，O是它的中心，过点O作BC平行的平面α，分别交AB，AC于点D，E，则四边形BCED的面积是（　　）

• A． $\frac{5\sqrt{3}}{9}$
• B． $\frac{4\sqrt{3}}{9}$
• C． $\frac{\sqrt{3}}{3}$
• D． $\frac{2\sqrt{3}}{3}$

Answer 1

分析 由已知得BC∥DE，$\frac{DE}{BC}=\frac{AO}{AE}$=$\frac{2}{3}$，由此求出DE，OE，从而能求出四边形BCED的面积．

解答 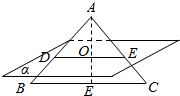解：∵△ABC是边长为2的正三角形，O是它的中心，
过点O作BC平行的平面α，分别交AB，AC于点D，E，
∴BC∥DE，$\frac{DE}{BC}=\frac{AO}{AE}$=$\frac{2}{3}$，
∴DE=$\frac{2}{3}×2=\frac{4}{3}$，OE=$\frac{1}{3}AE=\frac{1}{3}\sqrt{4-1}$=$\frac{\sqrt{3}}{3}$，
∴四边形BCED的面积S=$\frac{\frac{4}{3}+2}{2}×\frac{\sqrt{3}}{3}$=$\frac{5\sqrt{3}}{9}$．
故选：A．

点评 本题考查四边形面积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．