题目内容
1.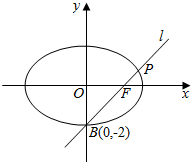 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,-2),斜率为1的直线l过它的右焦点F,且与椭圆相交于B、P两点.求:
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,-2),斜率为1的直线l过它的右焦点F,且与椭圆相交于B、P两点.求:(1)椭圆C的方程;
(2)以原点为顶点,坐标轴为对称轴,且过点P的抛物线方程.
分析 (1)由题意可得b=2,求得直线l的方程,代入B的坐标,可得c=2,再由a,b,c的关系,可得a,进而得到椭圆的方程;
(2)由直线方程y=x-2代入椭圆方程,求得P的坐标,再设过P的抛物线的方程为y2=mx或x2=ny,代入P的坐标,解方程可得m,n,进而得到抛物线的方程.
解答 解:(1)由题意可得b=2,
设右焦点F(c,0),设直线l的方程为y=x-c,
由题意可得0-c=-2,解得c=2,
即有a=$\sqrt{{b}^{2}+{c}^{2}}$=2$\sqrt{2}$,
则椭圆方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1;
(2)由直线方程y=x-2,代入椭圆方程,可得
3x2-8x=0,
解得x=0或$\frac{8}{3}$,
可得P($\frac{8}{3}$,$\frac{2}{3}$),
设过P的抛物线的方程为y2=mx或x2=ny,
即有$\frac{4}{9}$=$\frac{8}{3}$m,或$\frac{64}{9}$=$\frac{2}{3}$n,
解得m=$\frac{1}{6}$或n=$\frac{32}{3}$.
则所求抛物线的方程为y2=$\frac{1}{6}$x或x2=$\frac{32}{3}$y.
点评 本题考查椭圆和抛物线的方程的求法,注意运用待定系数法,考查运算能力,属于基础题,

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
16.下列四组函数中,表示相等函数的一组是( )
| A. | $f(x)=x,g(x)=\sqrt{x^2}$ | B. | f(x)=x,g(x)=|x| | C. | f(x)=x2-1,g(t)=t2-1 | D. | $f(x)=x,g(x)={(\sqrt{x})^2}$ |
5.同时掷两枚质地均匀的骰子,所得点数之和为6的概率等于( )
| A. | $\frac{1}{12}$ | B. | $\frac{5}{36}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{5}$ |