题目内容
10.已知直线l:(2+m)x+(1-m)y+4-m=0(1)若直线l的倾斜角为135°,求实数m的值;
(2)若直线l的横截距为-2,求实数m的值,;
(3)无论实数m取何时,直线恒过定点,求出定点坐标.
分析 (1)由直线l的倾斜角为135°,得到直线l的斜率为-1,由此能求出m的值.
(2)由直线l的横截距为-2,得到直线l过点(-2,0),由此能求出实数m的值.
(3)由已知得(x-y-1)m+(2x+y+4)=0,由无论实数m取何时,直线恒过定点,得到m的系数和x-y-1=0,由此能求出结果.
解答 解:(1)∵直线l:(2+m)x+(1-m)y+4-m=0的倾斜角为135°,
∴tan135°=-$\frac{2+m}{1-m}$=-1,解得m=-$\frac{1}{2}$.
∴m的值为-$\frac{1}{2}$.
(2)∵直线l:(2+m)x+(1-m)y+4-m=0的横截距为-2,
∴直线l过点(-2,0),
∴-2(2+m)+4-m=0,解得m=0.
∴实数m的值为0;
(3)∵(2+m)x+(1-m)y+4-m=0,
∴(x-y-1)m+(2x+y+4)=0,
∵无论实数m取何时,直线恒过定点,
∴$\left\{\begin{array}{l}{x-y-1=0}\\{2x+y+4=0}\end{array}\right.$,解得x=-1,y=-2.
∴无论实数m取何时,直线恒过定点(-1,-2).
点评 本题考查直线方程中参数值的求法,是基础题,解题时要注意直线的倾斜角、斜率、横截距离,直线恒过定点等知识点的合理运用.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
18.对函数f(x),若对于定义域中的任意三个数x1,x2,x3,都有f(x1),f(x2),f(x3)都能作为一个三角形三边的长,则称f(x)为“三角型函数”.已知函数f(x)=$\frac{{9}^{x}+m•{3}^{x}+1}{{9}^{x}+{3}^{x}+1}$为“三角型函数”.则实数m的取值范围是( )
| A. | [1,4] | B. | (-$\frac{1}{2}$,1) | C. | [-$\frac{1}{2}$,4] | D. | [1,2] |
15.已知点F1(-1,0),F2(1,0)为椭圆C的两个焦点,过点F2且垂直于x轴的直线与椭圆相交,设P为其中一交点,若△PF1F2为等腰三角形,则该椭圆的长轴长为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$+1 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{2}$+2 |
14.“lga>lgb”是“a>b”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
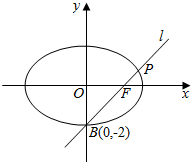 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,-2),斜率为1的直线l过它的右焦点F,且与椭圆相交于B、P两点.求:
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,-2),斜率为1的直线l过它的右焦点F,且与椭圆相交于B、P两点.求: