题目内容
10.四面体ABCD中,BD=$\sqrt{2}$,AB=AD=CB=CD=AC=1,求证:面ABD⊥面BCD.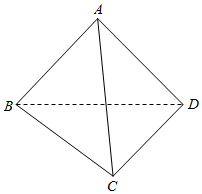
分析 取BD中点M,连结AM,CM,则AM⊥BD,CM⊥BD,利用勾股定理计算AM,CM,得出AM2+CM2=AC2,故AM⊥CM,于是AM⊥平面BCD,从而平面ABD⊥平面BCD.
解答 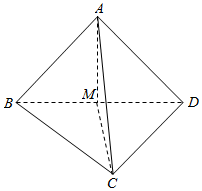 证明取BD中点M,连结AM,CM,
证明取BD中点M,连结AM,CM,
∵AB=AD=BC=CD=1,M是BC的中点,
∴AM⊥BD,CM⊥BD,BM=$\frac{1}{2}BC$=$\frac{\sqrt{2}}{2}$.
∴AM=$\frac{\sqrt{2}}{2}$,CM=$\frac{\sqrt{2}}{2}$,
又AC=1,∴AM2+CM2=AC2,
∴AM⊥CM,
又CM?平面BCD,BC?平面BCD,CM∩BC=M,
∴AM⊥平面BCD,
∵AM?平面ABD,
∴平面ABD⊥平面BCD.
点评 本题考查了面面垂直的判定,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知事件“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”发生的概率为$\frac{3}{5}$,则$\frac{AD}{AB}$=( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
18.已知复数z=$\frac{5{i}^{5}}{2-{i}^{3}}$-3i,则|z|等于( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
15.从双曲线$\frac{{x}^{2}}{a}$-y2=1的一个焦点F到向它的一条渐近线作垂线,垂足为A,O为原点.若△AOF的面积为1,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{7}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |