题目内容
18.已知复数z=$\frac{5{i}^{5}}{2-{i}^{3}}$-3i,则|z|等于( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 化简复数z,求出|z|即可.
解答 解:∵复数z=$\frac{5{i}^{5}}{2-{i}^{3}}$-3i=$\frac{5i}{2+i}$-3i=$\frac{5i(2-i)}{(2+i)(2-i)}$-3i=1-i,
∴|z|=$\sqrt{{1}^{2}{+(-1)}^{2}}$=$\sqrt{2}$.
故选:D.
点评 本题考查了复数的化简与求模问题,是基础题目.

练习册系列答案
相关题目
8.已知函数f(x)=b•ax(其中a,b为正实数且a≠1)的图象经过点A(1,27),B(-1,3)
(1)试求a、b的值;
(2)若不等式ax+bx≥m在x∈[1,+∞)时恒成立,求实数m的取值范围.
(1)试求a、b的值;
(2)若不等式ax+bx≥m在x∈[1,+∞)时恒成立,求实数m的取值范围.
7.式子$\frac{m(m+1)(m+2)…(m+20)}{20!}$可表示为( )
| A. | A${\;}_{m+20}^{20}$ | B. | C${\;}_{m+20}^{20}$ | C. | 21C${\;}_{m+20}^{20}$ | D. | 21C${\;}_{m+20}^{21}$ |
8.若在曲线y=a2x+x+1(a>0,且a≠1)上的点(0,m)处的切线与直线mx-y+1=0平行,则m+a=( )
| A. | 1+e | B. | 1+$\sqrt{e}$ | C. | 2+e | D. | 2+$\sqrt{e}$ |
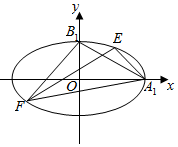 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,点E($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,设点A1,B1分别是椭圆的右顶点和上顶点,过点A1,B1引椭圆C的两条弦A1E、B1F.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,点E($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,设点A1,B1分别是椭圆的右顶点和上顶点,过点A1,B1引椭圆C的两条弦A1E、B1F.