题目内容
设a＝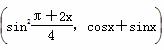
，b＝(4sinx，cosx－sinx)，f(x)＝a·b.
(1) 求函数f(x)的解析式；
(2) 已知常数ω＞0，若y＝f(ωx)在区间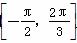
上是增函数，求ω的取值范围；
(3) 设集合A＝
，B＝{x||f(x)－m|＜2}，若AB，求实数m的取值范围．
解：(1) f(x)＝sin2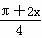
·4sinx＋(cosx＋sinx)·(cosx－sinx)
＝4sinx·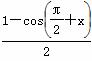
＋cos2x
＝2sinx(1＋sinx)＋1－2sin2x＝2sinx＋1，
所以所求解析式为f(x)＝2sinx＋1.
(2) ∵f(ωx)＝2sinωx＋1，ω＞0，
由2kπ－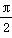
≤ωx≤2kπ＋，
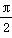得f(ωx)的增区间是
，k∈Z.
∵f(ωx)在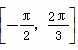
上是增函数，
∴
.
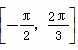
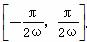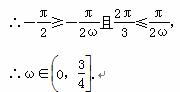
(3) 由|f(x)－m|＜2，得－2＜f(x)－m＜2，
即f(x)－2＜m＜f(x)＋2.
∵AB，∴当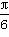
≤x≤
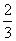π时，
不等式f(x)－2＜m＜f(x)＋2恒成立．
∴f(x)max－2＜m＜f(x)min＋2，
∵f(x)max＝f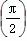
＝3，f(x)min＝f
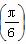＝2，
∴m∈(1，4)．
练习册系列答案
相关题目
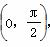，sinα＝
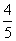，tan(α－β)＝－
，求cosβ的值．
(x∈R)的图象，只需把函数y＝2sinx(x∈R)的图象上所有的点经过怎样的变换得到？
<φ<
＝__________．
＝
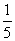，那么cosα＝________．
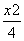＋y2＝1的左顶点为A，过A作两条互相垂直的弦AM、AN交椭圆于M、N两点．