题目内容
求sin210°＋cos240°＋sin10°cos40°的值．
解：(解法1)因为40°＝30°＋10°，于是原式＝sin210°＋cos2(30°＋10°)＋sin10°cos(30°＋10°)＝sin210°＋
＋sin10°·(
cos10°－
sin10°)＝
(sin210°＋cos210°)＝.
(解法2)设x＝sin210°＋cos240°＋sin10°cos40°，y＝cos210°＋sin240°＋cos10°sin40°.则x＋y＝1＋1＋sin10°cos40°＋cos10°sin40°＝2＋sin50°＝2＋cos40°，x－y＝cos80°－cos20°－＝－sin50°－＝－cos40°－.因此2x＝
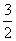，故x＝.
练习册系列答案
相关题目
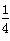.求：
，∠B＝2∠A.
，则cos2
＝________．
，且270°＜θ＜360°，则sin
＝________，cos
·cos
的最小正周期为________．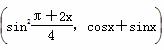
，b＝(4sinx，cosx－sinx)，f(x)＝a·b.
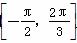上是增函数，求ω的取值范围；
，B＝{x||f(x)－m|＜2}，若AB，求实数m的取值范围．