题目内容
已知α、β∈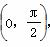 ,sinα=
,sinα=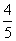 ,tan(α-β)=-
,tan(α-β)=- ,求cosβ的值.
,求cosβ的值.
解:∵ α、β∈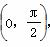 ,∴ -
,∴ - <α-β<
<α-β< .
.
又tan(α-β)=- <0,∴ -
<0,∴ - <α-β<0.
<α-β<0.
∴ =1+tan2(α-β)=
=1+tan2(α-β)= .
.
∴ cos(α-β)= ,sin(α-β)=-
,sin(α-β)=- .
.
又sinα=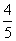 ,∴ cosα=
,∴ cosα=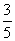 .
.
∴ cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)=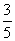 ×
× +
+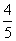 ×
× =
= .
.

练习册系列答案
相关题目
题目内容
已知α、β∈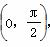 ,sinα=
,sinα=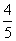 ,tan(α-β)=-
,tan(α-β)=- ,求cosβ的值.
,求cosβ的值.
解:∵ α、β∈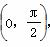 ,∴ -
,∴ - <α-β<
<α-β< .
.
又tan(α-β)=- <0,∴ -
<0,∴ - <α-β<0.
<α-β<0.
∴ =1+tan2(α-β)=
=1+tan2(α-β)= .
.
∴ cos(α-β)= ,sin(α-β)=-
,sin(α-β)=- .
.
又sinα=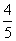 ,∴ cosα=
,∴ cosα=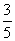 .
.
∴ cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)=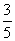 ×
× +
+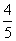 ×
× =
= .
.
