题目内容

数列{an}的前n项和Sn=2n2-1，则a5=
 
．
考点：数列递推式
专题：点列、递归数列与数学归纳法
分析：直接利用a5=S5-S4结合已知的Sn求得答案．
解答： 解：由Sn=2n2-1，得
a5=S5-S4=2×52-1-(2×42-1)=18．
故答案为：18．
点评：本题考查了数列递推式，考查了由数列的和求数列的通项，是基础题．
练习册系列答案
相关题目
已知π＜α＜α+β＜2π且cosα=-
12
13
，cos（α+β）=
17
2
26
，求角β．
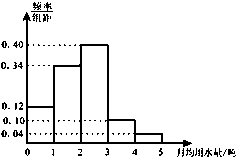如图是某城市通过抽样得到的居民某年的月均用水量（单位：吨）的频率分布直方图，其中分组区间为（0，1]，（1，2]，（2，3]，（3，4]，（4，5]．则由直方图可估计该城市居民月均用水量的众数是
 
，中位数是
 
．
已知函数f（x）=x2的定义域是{-2，1}，则该函数的值域是
 
．
已知|
a
|=4，|
b
|=
3
，（
a
+
b
）•（
a
-2
b
）=4，则
a
•
b
=
 
．
一个口袋内有4个不同的红球，6个不同的白球，若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于8分的取法有
 
种 （用数字作答）
给出以下命题，其中正确命题序号为
 
．
（1）若函数y=f（x）为偶函数，则函数y=f（x-1）的图象关于直线x=1 对称； 
（2）“x≠1”是“x2≠1”的充分不必要条件；
（3）函数y=2x-1的反函数为y=log2（x+1）其中x＞-1； 
（4）已知f′（x）是函数y=f（x）的导函数，若f′（x0）=0，则x0必为函数的极值点； 
（5）某城市现有人口a万人，预计人口年平均增长率为p．那么该城市第十年年初的人口总数为a（1+p）9万人．
下列命题正确的序号为
 
．
①空集无子集；
②任何一个集合至少有两个子集；
③空集是任何集合的真子集；
④∁U（∁UA）=A．
双曲线
x2
a2
-
y2
b2
=1（{a＞0，b＞0}）的渐近线为y=±
3
3
x，其顶点到渐近线的距离为1，则双曲线方程为（　　）
A、
x2
4
-
3y2
4
=1
B、
3x2
4
-
y2
4
=1
C、
x2
4
-
y2
4
=1
D、
x2
4
-
4y2
3
=1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网