题目内容
11.设函数f(x)=loga(1+x)-loga(1-x)的图象经过点(-$\frac{1}{2}$,-1).(1)求实数a;
(2)判断函数f(x)的奇偶数,并写出f($\frac{1}{2}$)的值.
分析 (1)根据函数f(x) 的图象经过点(-$\frac{1}{2}$,-1),可得loga(1-$\frac{1}{4}$)=-1,求得a的值.
(2)由于函数f(x)=${log}_{\frac{4}{3}}$(1-x2) 为偶函数,再利用f($\frac{1}{2}$)=f(-$\frac{1}{2}$),计算求的结果.
解答 解:(1)函数f(x)=loga(1+x)-loga(1-x)=loga(1-x2) 的图象经过点(-$\frac{1}{2}$,-1),
∴loga(1-$\frac{1}{4}$)=-1,求得a=$\frac{4}{3}$.
(2)由于函数f(x)=${log}_{\frac{4}{3}}$(1-x2) 为偶函数,f($\frac{1}{2}$)=f(-$\frac{1}{2}$)=-1.
点评 本题主要考查对数的运算性质,函数的奇偶性的判断,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
1.某几何的三视图如图所示,该几何体各个面中,面积最大的是( )
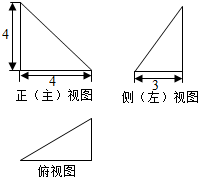

| A. | $2\sqrt{34}$ | B. | $8\sqrt{2}$ | C. | 10 | D. | $6\sqrt{2}$ |
19.已知⊙O1与⊙O2的半径分别为R、r,且它们是方程x2-9x+14=0的两根,若⊙O1与⊙O2相切,则圆心距O1O2等于( )
| A. | 5 | B. | 9 | C. | 5或9 | D. | 10或18 |
1.在△ABC中,如果(b+c+a)(b+c-a)=bc,那么A等于( )
| A. | 30° | B. | 120° | C. | 60° | D. | 150° |
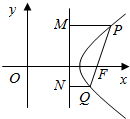 如图,点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,过点F的直线的斜率为3,与双曲线交于P,Q两点,分别过P、Q向右准线作垂线,垂足分别为M,N,且$\overrightarrow{PM}$=3$\overrightarrow{QN}$,求双曲线的离心率的大小.
如图,点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,过点F的直线的斜率为3,与双曲线交于P,Q两点,分别过P、Q向右准线作垂线,垂足分别为M,N,且$\overrightarrow{PM}$=3$\overrightarrow{QN}$,求双曲线的离心率的大小.