题目内容
6.自双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点 F1、F2分别向两条渐近线作垂线,垂足分别为A、B,连接AB,若梯形ABF2F1的面积为$\frac{3}{2}$,且ab=1,则双曲线的离心率为$\sqrt{2}$.分析 求出双曲线的焦点和渐近线方程,联立直线方程,可得垂足B的坐标,及A的坐标,运用梯形的面积公式和离心率公式,计算即可得到所求.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的焦点为F1(-c,0),F2(c,0),
渐近线方程为y=±$\frac{b}{a}$x,
由F2向渐近线y=$\frac{b}{a}$x作垂线交点为B,
由$\left\{\begin{array}{l}{y=\frac{b}{a}x}\\{y=-\frac{a}{b}(x-c)}\end{array}\right.$解得B($\frac{a}{bc}$,$\frac{1}{c}$),
即有A(-$\frac{a}{bc}$,$\frac{1}{c}$),
则梯形ABF2F1的面积为$\frac{1}{2}$(2c+$\frac{2a}{bc}$)•$\frac{1}{c}$=$\frac{3}{2}$,
即为2a=bc2,
又ab=1,即a=$\frac{1}{b}$,
c2=a2+b2,
可得a=b=1,c=$\sqrt{2}$,
即有e=$\frac{c}{a}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查双曲线的方程和性质,主要考查渐近线方程和离心率的求法,考查直线方程求交点,属于中档题.

练习册系列答案
相关题目
17.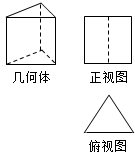 如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )
如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )
 如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )
如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )| A. | 8$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 4$\sqrt{3}$ |
14.已知f(x)是定义在R上周期为2的奇函数,当x∈(0,1)时,f(x)=3x-1,则f(log35)=( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | 4 | D. | $\frac{4}{9}$ |
1.已知f(x)+f(-x)=8,f(lg(log210))=5,则f(lg(lg2))=( )
| A. | -5 | B. | -1 | C. | 3 | D. | 4 |
18.有一组实验数据如表:
给出下列函数:①v=log${\;}_{\frac{1}{2}}$t;②v=$\sqrt{t}$;③v=($\frac{3}{2}$)t④y=$\frac{{t}^{2}-1}{2}$;
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是④(填序号).
| t | 1.99 | 3.0 | 4.0 | 5.1 | 6.12 |
| y | 1.50 | 4.04 | 7.50 | 12.00 | 18.01 |
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是④(填序号).