题目内容
已知tanα=2，求下列各式的值：
（1）
．
（2）
．
（3）4sin2α-3sinα•cosα-5cos2α．
（1）
| 2sinα-3cosα |
| 4sinα-9cosα |
（2）
| 2sin2α-3cos2α |
| 4sin2α-9cos2α |
（3）4sin2α-3sinα•cosα-5cos2α．
考点：三角函数的化简求值
专题：三角函数的求值
分析：（1）将所求的关系式中的“弦”化“切”，将tanα=2代入计算即可；
（2）将所求的关系式中的“弦”化“切”，再将tanα=2代入计算；
（3）将所求关系式化简为原式=
，再将tanα=2代入计算．
（2）将所求的关系式中的“弦”化“切”，再将tanα=2代入计算；
（3）将所求关系式化简为原式=
| 4tan2α-3tanα-5 |
| tan2α+1 |
解答：
解：（1）∵tanα=2，
∴
=
=-1；
（2）
=
=
=
；
（3）4sin2α-3sinαcosα-5cos2α=
=
=
=1．
∴
| 2sinα-3cosα |
| 4sinα-9cosα |
| 2tanα-3 |
| 4tanα-9 |
（2）
| 2sin2α-3cos2α |
| 4sin2α-9cos2α |
| 2tan2α-3 |
| 4tan2α-9 |
| 2×22-3 |
| 4×22-9 |
| 5 |
| 7 |
（3）4sin2α-3sinαcosα-5cos2α=
| 4sin2α-3sinαcosα-5cos2α |
| sin2α+cos2α |
| 4tan2α-3tanα-5 |
| tan2α+1 |
| 4×22-3×2-5 |
| 4+1 |
点评：本题考查三角函数的化简求值，将所求的关系式中的“弦”化“切”是关键，属于基础题．
练习册系列答案
相关题目
如图所示的几何体是由一个棱长为2的正四面体和一个半圆锥组成，点O为半圆的圆心，E为BC的中点．
如图，已知ABCD是圆锥SO底面圆O的内接矩形．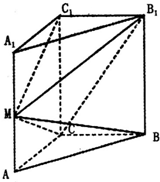
如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，2AC=AA1=BC=2，M为AA1的中点．
如图，函数f（x）的图象是折线段ABC，其中点A，B，C的坐标分别为（0，4），（2，0），（6，4），则f{f[f（3）]}=