题目内容
已知椭圆的方程为
+
=1,过右焦点F的直线交椭圆于A、B两点,则
取值范围为 .
| x2 |
| 25 |
| y2 |
| 16 |
| |FA| |
| |FB| |
考点:椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:求出椭圆的方程为
+
=1,a=5,c=3.根据椭圆的性质,|FA|,|FB|的最大值为a+c=8,最小值为a-c=2,即可得出结论.
| x2 |
| 25 |
| y2 |
| 16 |
解答:
解:∵椭圆的方程为
+
=1,
∴a=5,c=3.
根据椭圆的性质,|FA|、|FB|的最大值为a+c=8,最小值为a-c=2,
∴
取值范围为[
,4].
故答案为:[
,4].
| x2 |
| 25 |
| y2 |
| 16 |
∴a=5,c=3.
根据椭圆的性质,|FA|、|FB|的最大值为a+c=8,最小值为a-c=2,
∴
| |FA| |
| |FB| |
| 1 |
| 4 |
故答案为:[
| 1 |
| 4 |
点评:本题考查椭圆的性质,考查学生的十计算能力,正确运用椭圆的性质是关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线的极坐标方程为θ=
(ρ∈R),它与圆
(α为参数)相切,则|a-b|= .
| π |
| 4 |
|
已知点(3,1)和(-1,5)在直线3x-2y+a=0的两侧,则a的取值范围是( )
| A、a<-7或 a>13 |
| B、-7<a<13 |
| C、a=7 或 a=13 |
| D、-13<a<7 |
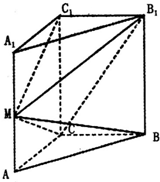 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,M为AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,M为AA1的中点. 如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(3)]}=
如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(3)]}=