题目内容
已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R}
(1)求A∩B=[1,3],求实数m的值.
(2)若A⊆B,求实数m的取值范围.
(1)求A∩B=[1,3],求实数m的值.
(2)若A⊆B,求实数m的取值范围.
考点:集合的包含关系判断及应用,交集及其运算
专题:计算题,集合
分析:(1)将集合A,B进行化简,利用A∩B=[1,3]建立不等关系,求实数m的值即可;
(2)利用A⊆B,可得
,即可求实数m的取值范围.
(2)利用A⊆B,可得
|
解答:
解:(1)A={x|x2-2x-3≤0,x∈R}={x|-1≤x≤3},
B={x|x2-2mx+m2-4≤0,x∈R}={x|m-2≤x≤m+2}
∵A∩B=[1,3],
∴m-2=1,解得m=3;
(2)∵A⊆B,
∴
,∴m=1.
B={x|x2-2mx+m2-4≤0,x∈R}={x|m-2≤x≤m+2}
∵A∩B=[1,3],
∴m-2=1,解得m=3;
(2)∵A⊆B,
∴
|
点评:本题主要考查集合关系的应用,先将集合A,B进行化简是解决本题的关键,注意对区间端点值等号的取舍问题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
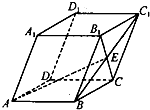 如图,在平行六面体ABCD-A1B1C1D1中,E为BC1与B1C的交点,记
如图,在平行六面体ABCD-A1B1C1D1中,E为BC1与B1C的交点,记| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| AE |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
已知两非零向量
=(a1,b1),
=(a2,b2),其中a1,a2,b1,b2均为实数,集合A={x|a1x+b1≥0},集合B={x|a2x+b2≥0},则“
∥
”是“A=B”的( )
| a |
| b |
| a |
| b |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |