题目内容
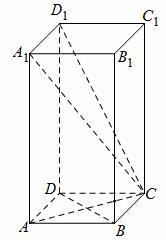
已知正四棱柱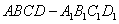 中,
中,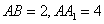 .
.
(Ⅰ)求证: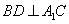 ;
;
(Ⅱ)求二面角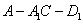 的余弦值;
的余弦值;
(Ⅲ)在线段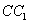 上是否存在点
上是否存在点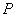 ,使得平面
,使得平面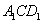
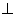 平面
平面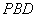 ,若存在,求出
,若存在,求出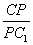 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
证明:(Ⅰ)因为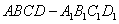 为正四棱柱,
为正四棱柱,
所以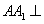 平面
平面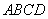 ,且
,且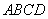 为正方形. ………1分
为正方形. ………1分
因为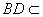 平面
平面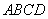 ,
,
所以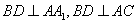 . ………2分
. ………2分
因为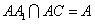 ,
,
所以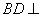 平面
平面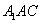 . ………3分
. ………3分
因为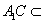 平面
平面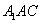 ,
,
所以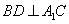 . ………4分
. ………4分
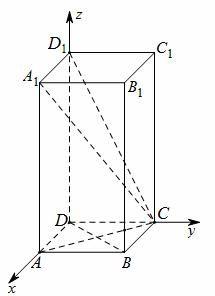
(Ⅱ) 如图,以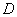 为原点建立空间直角坐标系
为原点建立空间直角坐标系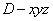 .则
.则
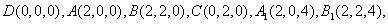
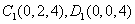 ………5分
………5分
所以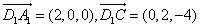 .
.
设平面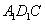 的法向量
的法向量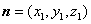 .
.
所以 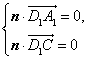 .即
.即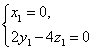 ……6分
……6分
令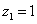 ,则
,则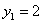 .
.
所以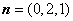 .
.
由(Ⅰ)可知平面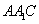 的法向量为
的法向量为 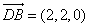 . ……7分
. ……7分
所以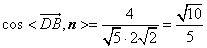 . ……8分
. ……8分
因为二面角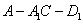 为钝二面角,
为钝二面角,
所以二面角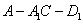 的余弦值为
的余弦值为 . ………9分
. ………9分
(Ⅲ)设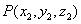 为线段
为线段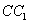 上一点,且
上一点,且 .
.
因为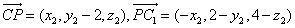 .
.
所以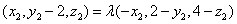 . ………10分
. ………10分
即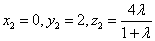 .
.
所以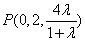 . ………11分
. ………11分
设平面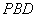 的法向量
的法向量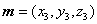 .
.
因为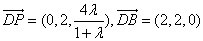 ,
,
所以 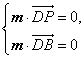 .即
.即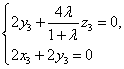 . ………12分
. ………12分
令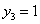 ,则
,则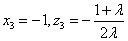 .
.
所以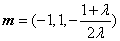 . ………13分
. ………13分
若平面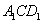
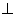 平面
平面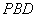 ,则
,则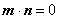 .
.
即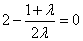 ,解得
,解得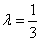 .
.
所以当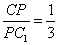 时,平面
时,平面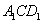
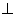 平面
平面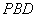 . ………14分
. ………14分

 cos B·cos C,且tan B·tan C=1-
cos B·cos C,且tan B·tan C=1-
 中,
中, 是
是 的中点,
的中点, 为线段
为线段 上一动点,则
上一动点,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
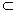 α,n
α,n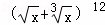 展开式中有理项共有 项.
展开式中有理项共有 项. 在点
在点 处的切线与
处的切线与 轴、直线
轴、直线 所围成的三角形的面积为( )
所围成的三角形的面积为( ) B.
B. C.
C. D.
D.
 ,集合A={
,集合A={ },B={
},B={ },若
},若 =R,则
=R,则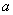 的取值范围为( )
的取值范围为( ) ,-2) B.(-
,-2) B.(- 有且仅有一个正实数零点,则实数
有且仅有一个正实数零点,则实数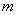 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.