题目内容
14.现阶段全国多地空气质量指数“爆表”.为探究车流量与PM2.5浓度是否相关,现对北方某中心城市的车流量最大的地区进行检测,现采集到12月某天7个不同时段车流量与PM2.5浓度的数据,如下表:| 车流量x(万辆/小时) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5浓度y(微克/立方米) | 30 | 36 | 38 | 40 | 42 | 44 | 50 |
(2)规定当PM2.5浓度平均值在(0,50],空气质量等级为优;当PM2.5浓度平均值在(50,100],空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
附:回归直线方程:$\widehaty=\widehatbx+\widehata$,其中$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y=\widehatb\overline x$.
分析 (1)根据上表中的数据,用最小二乘法求出回归系数,即可求出y关于x的线性回归方程;
(2)利用$\frac{20}{7}x+\frac{200}{7}$≤100,即可得出结论.
解答 解:(1)∵$\overline x=4,\overline y=40$,$\sum_{i=1}^7{{x_i}{y_i}=1200,\sum_{i=1}^7{{x_i}^2=140}}$,
∴$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$=$\frac{20}{7}$,$\widehata=\overline y=\widehatb\overline x$=$\frac{200}{7}$,
故y关于x的线性回归方程是:y=$\frac{20}{7}x+\frac{200}{7}$;
(2)$\frac{20}{7}x+\frac{200}{7}$≤100即x≤25,即预测要将车流量控制在每小时25万辆内..
点评 本题考查回归方程,考查利用数学知识解决实际问题的能力,正确计算是关键.

练习册系列答案
相关题目
5.已知函数f(x)=log2x,x∈[1,8],则不等式1≤f(x)≤2成立的概率是( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
9.已知点A(-1,1),B(1,2),C(2,3),且$\overrightarrow{AB}⊥({\overrightarrow{BC}+λ\overrightarrow{AC}})$,则λ=( )
| A. | $\frac{3}{8}$ | B. | $-\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
6.设F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,双曲线上存在一点P使得∠F1PF2=60°,|OP|=3b(O为坐标原点),则该双曲线的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{7}{6}$ | D. | $\frac{\sqrt{42}}{6}$ |
4.函数f(x)=sin(πx+θ)(|θ|<$\frac{π}{2}$)的部分图象如图,且f(0)=-$\frac{1}{2}$,则图中m的值为( )
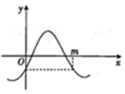

| A. | 1 | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{4}{3}$或2 |
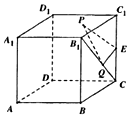 如右图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,点P,Q分别为面A1B1C1D1和线段B1C上的动点,则△PEQ周长的最小值为$\sqrt{10}$.
如右图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,点P,Q分别为面A1B1C1D1和线段B1C上的动点,则△PEQ周长的最小值为$\sqrt{10}$. 如图所示的空间几何体中,底面四边形ABCD为正方形,AF⊥AB,AF∥BE,平面ABEF⊥平面ABCD,DF=$\sqrt{5}$,CE=2$\sqrt{2}$,BC=2.
如图所示的空间几何体中,底面四边形ABCD为正方形,AF⊥AB,AF∥BE,平面ABEF⊥平面ABCD,DF=$\sqrt{5}$,CE=2$\sqrt{2}$,BC=2.