题目内容
18.已知不等式组$\left\{\begin{array}{l}x+y≥4\\ x-y≥-2\\ x≤2\end{array}\right.$,表示的平面区域为D,点O(0,0)、A(1,0),若M是D上的动点,则向量$\overrightarrow{OA}$在向量$\overrightarrow{OM}$方向上的投影的最小值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
分析 由约束条件作出可行域,设向量$\overrightarrow{OA}$与向量$\overrightarrow{OM}$的夹角为θ,求得向量$\overrightarrow{OA}$在向量$\overrightarrow{OM}$方向上的投影z=$|\overrightarrow{OA}|cosθ$.数形结合求出cosθ的最小值得答案.
解答 解:设M(x,y),则$\overrightarrow{OA}=(1,0),\overrightarrow{OM}=(x,y)$,
再设向量$\overrightarrow{OA}$与向量$\overrightarrow{OM}$的夹角为θ,
则向量$\overrightarrow{OA}$在向量$\overrightarrow{OM}$方向上的投影z=$|\overrightarrow{OA}|cosθ$.
由约束条件$\left\{\begin{array}{l}x+y≥4\\ x-y≥-2\\ x≤2\end{array}\right.$作出可行域如图,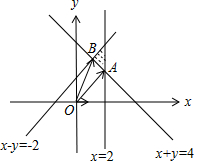
联立$\left\{\begin{array}{l}{x-y=-2}\\{x+y=4}\end{array}\right.$,解得B(1,3),
∴cosθ的最小值为$\frac{\sqrt{10}}{10}$.
∴向量$\overrightarrow{OA}$在向量$\overrightarrow{OM}$方向上的投影z=$|\overrightarrow{OA}|cosθ$的最小值为1×$\frac{\sqrt{10}}{10}=\frac{\sqrt{10}}{10}$.
故选:C.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
| A. | 0≤a<1 | B. | -1<a<1 | C. | 0<a<1 | D. | $0<a<\frac{1}{2}$ |
| A. | {1,3,5} | B. | {2,4,6} | C. | {1,5} | D. | {1,6} |
| A组 | B组 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
(Ⅱ)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“A组”和“B组”的人数;
(Ⅲ)从(Ⅱ)中抽取的5人中再随机抽取3人赠送200元的护肤品套装,求“这3人中既有A组又有B组”的概率.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
参考数据:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| $\overrightarrow{OA}•\overrightarrow{OB}=0$ | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
| A. | 216种 | B. | 288种 | C. | 360种 | D. | 432种 |