题目内容
7.已知cosα=$\frac{3}{5}$,cos(α-β)=$\frac{{7\sqrt{2}}}{10}$,且0<β<α<$\frac{π}{2}$,那么β=( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
分析 由α和β的范围,求出β-α的范围,然后由cosα和cos(α-β)的值,利用同角三角函数间的基本关系求出sinα和sin(β-α)的值,然后由β=(β-α)+α,利用两角和的余弦函数公式化简后,根据特殊角的三角函数值即可求出β的度数.
解答 解:由0<α<β<$\frac{π}{2}$,得到0<β-α<$\frac{π}{2}$,又cosα=$\frac{3}{5}$,cos(α-β)=cos(β-α)=$\frac{{7\sqrt{2}}}{10}$,
所以sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{4}{5}$,sin(β-α)=-sin(α-β)=-$\sqrt{1-co{s}^{2}(α-β)}$=-$\frac{\sqrt{2}}{10}$,
则cosβ=cos[(β-α)+α]
=cos(β-α)cosα-sin(β-α)sinα
=$\frac{{7\sqrt{2}}}{10}$×$\frac{3}{5}$-(-$\frac{\sqrt{2}}{10}$)×$\frac{4}{5}$=$\frac{\sqrt{2}}{2}$,
所以β=$\frac{π}{4}$.
故选:C.
点评 此题考查学生灵活运用同角三角函数间的基本关系及两角和的余弦函数公式化简求值,是一道基础题.做题时注意角度的变换,属于基础题.

练习册系列答案
相关题目
17.已知集合A={x|log2x≥0},B={x|log2(x-1)≤2},则集合A∩B=( )
| A. | {1,2,3} | B. | {1,3} | C. | (1,3] | D. | (1,5] |
18.某人准备投资1200万元办一所中学,为了考虑社会效益和经济效益,对该地区教育市场进行调查,得出一组数据,列表如下(以班级为单位).
市场调查表:
根据物价部门的有关规定:初中是义务教育阶段,收费标准适当控制,预计除书本费、办公费外,初中每人每年可收取600元.高中每人每年可收取1500元.因生源和环境等条件限制,办学规模以20至30个班为宜(含20个班与30个),教师实行聘任制.初、高中教育周期均为三年,设初中编制为x个班,高中编制为y个班,请你合理地安排招生计划,使年利润最大.
市场调查表:
| 班级学生数 | 配备教师数 | 硬件建设费(万元) | 教师年薪(万元) | |
| 初中 | 50 | 2.0 | 28 | 1.2 |
| 高中 | 40 | 2.5 | 58 | 1.6 |
15.由曲线y=x2,y=$\sqrt{x}$围成的封闭图形的面积为( )
| A. | $\frac{1}{6}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
18.已知不等式组$\left\{\begin{array}{l}x+y≥4\\ x-y≥-2\\ x≤2\end{array}\right.$,表示的平面区域为D,点O(0,0)、A(1,0),若M是D上的动点,则向量$\overrightarrow{OA}$在向量$\overrightarrow{OM}$方向上的投影的最小值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
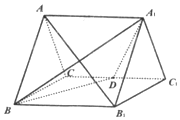 直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.