题目内容
6.已知函数$f(x)=\frac{1}{2}{x^2}-alnx+1$在(0,1)内有最小值,则a的取值范围是( )| A. | 0≤a<1 | B. | -1<a<1 | C. | 0<a<1 | D. | $0<a<\frac{1}{2}$ |
分析 由函数f(x)在(0,1)内有最小值,可得f′(x)≥0在(0,1)上由极小值.利用导函数的单调性求出即可
解答 解:函数$f(x)=\frac{1}{2}{x^2}-alnx+1$,(a∈R).f′(x)=x-$\frac{a}{x}$,
∵函数f(x)在(0,1)内有最小值,
∴f′(x)=0在(0,1)上有解.函数有极小值也为最小值.
∴x-$\frac{a}{x}$=0,x∈(0,1)?$\sqrt{a}$<1,a∈(0,1).
并且x$∈(0,\sqrt{a})$,f′(x)<0,x∈($\sqrt{a}$,1),f′(x)>0,
x=$\sqrt{a}$函数取得最小值也极小值.
∴0<a<1.
故选:C.
点评 熟练掌握利用导数研究函数的单调性、函数的极值,等价转化、考查计算能力.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
15.由曲线y=x2,y=$\sqrt{x}$围成的封闭图形的面积为( )
| A. | $\frac{1}{6}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
14.我国古代数学有非常高的成就,在很多方面都领先于欧洲数学.下面数学名词中蕴含微积分中“极限思想”的是( )
| A. | 天元术 | B. | 少广术 | C. | 衰分术 | D. | 割圆术 |
1.有一段演绎推理:若直线平行于平面,则这条直线平行于平面内所有直线;≠已知直线b∥平面α,直线a?平面α;则直线b∥直线a”下列叙述正确的是( )
| A. | 该命题是真命题 | |
| B. | 该命题是假命题,因为大前提是错误的 | |
| C. | 该命题是假命题,因为小前提是错误的 | |
| D. | 该命题是假命题,因为结论是错误的 |
18.已知不等式组$\left\{\begin{array}{l}x+y≥4\\ x-y≥-2\\ x≤2\end{array}\right.$,表示的平面区域为D,点O(0,0)、A(1,0),若M是D上的动点,则向量$\overrightarrow{OA}$在向量$\overrightarrow{OM}$方向上的投影的最小值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
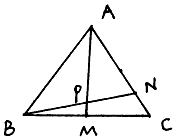 如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=3NC,AM与BN相交于点P,设$\overrightarrow{CA}$=$\overrightarrow a$,$\overrightarrow{CB}$=$\overrightarrow b$,用$\overrightarrow a$、$\overrightarrow b$表示$\overrightarrow{CP}$.
如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=3NC,AM与BN相交于点P,设$\overrightarrow{CA}$=$\overrightarrow a$,$\overrightarrow{CB}$=$\overrightarrow b$,用$\overrightarrow a$、$\overrightarrow b$表示$\overrightarrow{CP}$.