题目内容
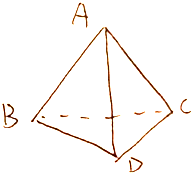 如图三棱锥A-BCD中DC⊥BC,BC=2
如图三棱锥A-BCD中DC⊥BC,BC=2| 3 |
| 2 |
(1)证明:平面ABC⊥平面ACD;
(2)求二面角A-BD-C的余弦值.
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知条件利用勾股定理得CD⊥AC,AB⊥AD,从而CD⊥平面ABC,进而AB⊥CD,由此得到AB⊥平面ADC,从而能证明平面ABC⊥平面ADC.
(2)由CD⊥平面ABC,且CD?平面BDC,得平面ABC⊥平面BDC,过点A作AE⊥平面BDC,交BC于E,过E作EF⊥BD,交BD于F,连结AF,由三垂线定理,得∠AFE是二面角A-BD-C的平面角,由此能求出二面角A-BD-C的余弦值.
(2)由CD⊥平面ABC,且CD?平面BDC,得平面ABC⊥平面BDC,过点A作AE⊥平面BDC,交BC于E,过E作EF⊥BD,交BD于F,连结AF,由三垂线定理,得∠AFE是二面角A-BD-C的平面角,由此能求出二面角A-BD-C的余弦值.
解答:
 (1)证明:∵三棱锥A-BCD中DC⊥BC,
(1)证明:∵三棱锥A-BCD中DC⊥BC,
BC=2
,CD=AC=2,AB=AD=2
,
∴BD=
=4,AC2+CD2=AD2,
∴AB2+AD2=BD2,∴CD⊥AC,AB⊥AD,
又AC∩BC=C,∴CD⊥平面ABC,
又AB?平面ABC,∴AB⊥CD,
又CD∩AD=D,∴AB⊥平面ADC,
又AB?平面ABC,∴平面ABC⊥平面ADC.
(2)解:∵CD⊥平面ABC,且CD?平面BDC,
∴平面ABC⊥平面BDC,
过点A作AE⊥平面BDC,交BC于E,过E作EF⊥BD,交BD于F,
连结AF,由三垂线定理,得∠AFE是二面角A-BD-C的平面角,
∵AB⊥AC,AB=2
,AC=2,BC=2
,
∴AE=
=
=
,
∵AB=AD=2
,BD=4,AF⊥BD,∴AF=
=2,
∴cos∠AFE=
=
=
,
∴二面角A-BD-C的余弦值为
.
 (1)证明:∵三棱锥A-BCD中DC⊥BC,
(1)证明:∵三棱锥A-BCD中DC⊥BC,BC=2
| 3 |
| 2 |
∴BD=
| BC2+DC2 |
∴AB2+AD2=BD2,∴CD⊥AC,AB⊥AD,
又AC∩BC=C,∴CD⊥平面ABC,
又AB?平面ABC,∴AB⊥CD,
又CD∩AD=D,∴AB⊥平面ADC,
又AB?平面ABC,∴平面ABC⊥平面ADC.
(2)解:∵CD⊥平面ABC,且CD?平面BDC,
∴平面ABC⊥平面BDC,
过点A作AE⊥平面BDC,交BC于E,过E作EF⊥BD,交BD于F,
连结AF,由三垂线定理,得∠AFE是二面角A-BD-C的平面角,
∵AB⊥AC,AB=2
| 2 |
| 3 |
∴AE=
| AB×AC |
| BC |
2
| ||
2
|
2
| ||
| 3 |
∵AB=AD=2
| 2 |
(2
|
∴cos∠AFE=
| AE |
| AF |
| ||||
| 2 |
| ||
| 3 |
∴二面角A-BD-C的余弦值为
| ||
| 3 |
点评:本题考查平面与平面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
命题“对任意 x∈R,都有 x2≥0”的否定为( )
| A、对任意 x∈R,都有 x2<0 |
| B、不存在 x∈R,使得 x2<0 |
| C、存在 x0∈R,使得 x02≥0 |
| D、存在 x0∈R,使得 x02<0 |
在正四棱柱ABCD-A′B′C′D′中,AB=1,A′A=2,则 A′C与BC所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知椭圆C:
+x2=1,直线l:9x+y-5=0与椭圆C相交于A、B两点,点P为弦AB的中点,则点P的坐标为( )
| y2 |
| 9 |
A、(
| ||||
B、(-
| ||||
| C、(1,-4) | ||||
| D、(-1,14) |
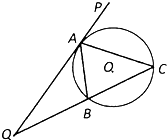 如图,直线 PQ与⊙O相切于点 A,A B是⊙O的弦,∠P A B的平分线 AC交⊙O于点C,连结C B,并延长与直线 PQ相交于点Q.
如图,直线 PQ与⊙O相切于点 A,A B是⊙O的弦,∠P A B的平分线 AC交⊙O于点C,连结C B,并延长与直线 PQ相交于点Q. 图中的程序框图所描述的算法称为欧几里得辗转相除法. 若输入m=209,n=121,则输出m=
图中的程序框图所描述的算法称为欧几里得辗转相除法. 若输入m=209,n=121,则输出m=