题目内容
7.设m,n是两条不同的直线,α,β是不同的平面,则下列命题中正确的是( )| A. | 若α⊥β,m?α,n?β,则m⊥n | B. | 若α∥β,m?α,n?β,则m∥n | ||
| C. | 若m⊥n,m?α,n?β,则α⊥β | D. | 若m⊥α,m∥n,n∥β,则α⊥β |
分析 在A中,m与n相交、平行或异面;在B中,m与n平行或异面;在C中,α与β相交或平行;在D中,由面面垂直的判定定理得α⊥β.
解答 解:由m,n是两条不同的直线,α,β是不同的平面,知:
在A中:若α⊥β,m?α,n?β,则m与n相交、平行或异面,故A错误;
在B中:若α∥β,m?α,n?β,则m与n平行或异面,故B错误;
在C中:若m⊥n,m?α,n?β,则α与β相交或平行,故C错误;
在D中:若m⊥α,m∥n,n∥β,则由面面垂直的判定定理得α⊥β,故D正确.
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
17.如图,在△ABC中,$\overrightarrow{BD}=2\overrightarrow{DC}$,若$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}=\overrightarrow b$,则$\overrightarrow{AD}$=( )
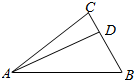

| A. | $\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | B. | $\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$ | D. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ |
15.给出函数f(x)=a2x-1+2(a为常数,且a>0,a≠1),无论a取何值,函数f(x)恒过定点P,则P的坐标是( )
| A. | (0,1) | B. | (1,2) | C. | (1,3) | D. | ($\frac{1}{2}$,3) |
12.对甲、乙两个班级的某次数学成绩进行统计,按照大于等于85分为优秀,85分以下为非优秀,得到如下所示的列联表:
已知在全部的105人中随机抽取1人,成绩优秀的概率为$\frac{2}{7}$.
(1)求b,c的值;
(2)根据表闻表中的数据,运用独立检验的思想方法分析:学生的数学成绩与班级是否有关系?并说明理由.
附:参考公式与临界值表:K2=$\frac{n(ab-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | b | |
| 乙班 | c | 30 | |
| 总计 | 105 |
(1)求b,c的值;
(2)根据表闻表中的数据,运用独立检验的思想方法分析:学生的数学成绩与班级是否有关系?并说明理由.
附:参考公式与临界值表:K2=$\frac{n(ab-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥K0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
19.从装有3个红球和3个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是( )
| A. | 恰有1个红球与恰有2个红球 | B. | 至少有1个黑球与都是黑球 | ||
| C. | 至少有1个黑球与至少有1个红球 | D. | 至多有1个黑球与都是红球 |