题目内容
以下列结论中：
（1）|
•
|≤|
||
|；
（2）
(
•
)=
2
；
（3）如果
•
＜0，那么
与
的夹角为钝角；
（4）若
是直线l的方向向量，则λ
(λ∈R)也是直线l的方向向量；
（5）
•
=
•
是
=
的必要不充分条件．
正确结论的序号是 ．
（1）|
| a |
| b |
| a |
| b |
（2）
| a |
| a |
| b |
| a |
| b |
（3）如果
| a |
| b |
| a |
| b |
（4）若
| a |
| a |
（5）
| a |
| b |
| b |
| c |
| b |
| 0 |
正确结论的序号是
考点：平面向量数量积的运算,必要条件、充分条件与充要条件的判断
专题：平面向量及应用
分析：（1）利用向量的数量积和余弦函数的有界性可得：|
•
|=||
| |
|cos＜
，
＞|≤|
||
|；
（2）由于
•
与
2都为实数，而
与
不一定共线，即可判断出；
（3）如果
•
＜0，那么
与
的夹角为钝角或平角；
（4）若
是直线l的方向向量，则λ
(λ∈R)不一定是直线l的方向向量，当λ=0时不满足；
（5）当
=
时
•
=
•
成立，反之不一定成立，即可得出．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
（2）由于
| a |
| b |
| a |
| a |
| b |
（3）如果
| a |
| b |
| a |
| b |
（4）若
| a |
| a |
（5）当
| b |
| 0 |
| a |
| b |
| b |
| c |
解答：
解：（1）∵|
•
|=||
| |
|cos＜
，
＞|≤|
||
|，因此正确；
（2）∵
•
与
2都为实数，而
与
不一定共线，因此不成立；
（3）如果
•
＜0，那么
与
的夹角为钝角或平角，因此不正确；
（4）若
是直线l的方向向量，则λ
(λ∈R)不一定是直线l的方向向量，当λ=0时不满足；
（5）当
=
时
•
=
•
成立，反之不一定成立，因此
•
=
•
是
=
的必要不充分条件，故正确．
综上可知：只有（1）（5）正确．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
（2）∵
| a |
| b |
| a |
| a |
| b |
（3）如果
| a |
| b |
| a |
| b |
（4）若
| a |
| a |
（5）当
| b |
| 0 |
| a |
| b |
| b |
| c |
| a |
| b |
| b |
| c |
| b |
| 0 |
综上可知：只有（1）（5）正确．
点评：本题综合考查了向量的数量积、向量共线定理、向量夹角公式、充分必要条件，属于中档题．
练习册系列答案
小学课时特训系列答案
相关题目
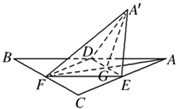如图，正△ABC的中线AF与中位线DE相交于G，已知△A′ED是△AED绕DE旋转过程中的一个图形．其中正确的说法是（ ）（1）动点A′在平面ABC上的射影在线段AF上
（2）恒有平面A′GF⊥平面BCED
（3）三棱锥A′-FED的体积有最大值
（4）异面直线A′E与BD不可能垂直．
| A、（1）（2）（3） |
| B、（1）（2）（4） |
| C、（2）（3）（4） |
| D、（1）（3）（4） |
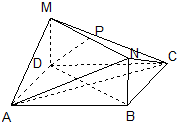在如图所示的几何体中，四边形ABCD和BDMN都是矩形，且MD⊥平面ABCD，P是MN的中点．若AB=4，BC=3，MD=1，
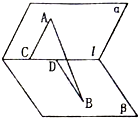如图，在60°的两面角α-l-β中，A∈α，B∈β，AC⊥l与C，BD⊥l于D，AC=2，BD=3，AB=5，则CD=
如图甲，△ABC是边长为6的等边三角形，E，D分别为AB、AC靠近B、C的三等分点，点G为BC边的中点．线段AG交线段ED于F点，将△AED沿ED翻折，使平面AED⊥平面BCDE，连接AB、AC、AG形成如图乙所示的几何体．