题目内容
在下列命题
①?x∈R,(
)x>0;
②“α=
”是“sinα=1”的充要条件;
③(
+
)4展开式中的常数项为2;
④设随机变量ξ~N(0,1),若P(ξ≥1)=p,则P(-1<ξ<0)=
-p.
其中所有正确命题的序号是( )
①?x∈R,(
| 1 |
| 2 |
②“α=
| π |
| 2 |
③(
| x3 |
| 2 |
| 1 |
| x |
④设随机变量ξ~N(0,1),若P(ξ≥1)=p,则P(-1<ξ<0)=
| 1 |
| 2 |
其中所有正确命题的序号是( )
| A、①②③ | B、①③④ |
| C、①②④ | D、②③④ |
考点:命题的真假判断与应用
专题:函数的性质及应用,概率与统计,二项式定理
分析:根据指数函数的性质可以判定①是否正确,根据三角函数的性质可以判定②是否正确;
根据二项展开式可以判定③是否正确,根据正态分布的知识可以判定④是否正确.
根据二项展开式可以判定③是否正确,根据正态分布的知识可以判定④是否正确.
解答:
解:①中,根据指数函数的性质知,“?x∈R,(
)x>0”是正确的;
②中,当α=
时,sinα=sin
=1,当sinα=1时,α=
+2kπ,其中k∈Z;应是充分不必要条件,∴命题错误;
③中,(
+
)4展开式Tr=
(
)4-r•(
)r=
(
)4-r•x12-4r,令12-4r=0,
∴r=3,∴T3=
×
=2,∴常数项为2,命题正确;
④中,随机变量ξ~N(0,1),∵P(ξ≥1)=p,∴P(-1<ξ<0)=
-p,命题正确;
以上正确命题的序号是①③④;
故选:B.
| 1 |
| 2 |
②中,当α=
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
③中,(
| x3 |
| 2 |
| 1 |
| x |
| C | r 4 |
| x3 |
| 2 |
| 1 |
| x |
| C | r 4 |
| 1 |
| 2 |
∴r=3,∴T3=
| C | 3 4 |
| 1 |
| 2 |
④中,随机变量ξ~N(0,1),∵P(ξ≥1)=p,∴P(-1<ξ<0)=
| 1 |
| 2 |
以上正确命题的序号是①③④;
故选:B.
点评:本题考查了指数函数、三角函数、二项展开式以及正态分布的有关知识,是综合题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 按照如图的程序框图执行,若输出结果为31,则M处的条件为( )
按照如图的程序框图执行,若输出结果为31,则M处的条件为( )| A、k≥32 | B、k<16 |
| C、k<32 | D、k≥16 |
设z=
,若复数z为纯虚数(其中i是虚数单位),则实数a等于( )
| 1-ai |
| i |
| A、-1 | ||
| B、0 | ||
| C、1 | ||
D、
|
如图是一个算法框图,则输出的k的值是( )


| A、5 | B、6 | C、7 | D、8 |
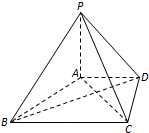 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=