题目内容
已知圆C:x2+y2+4x+4y+m=0,直线l:x+y+2=0.
(1)若圆C与直线l相离,求m的取值范围;
(2)若圆D过点P(1,1),且与圆C关于直线l对称,求圆D的方程.
(1)若圆C与直线l相离,求m的取值范围;
(2)若圆D过点P(1,1),且与圆C关于直线l对称,求圆D的方程.
考点:直线与圆的位置关系,圆的标准方程
专题:直线与圆
分析:(1)求出圆C的圆心与直线l相离,通过距离大于半径,即可求m的取值范围;
(2)通过圆D过点P(1,1),以及求出圆C关于直线l对称的对称点,求出圆的半径即可求圆D的方程.
(2)通过圆D过点P(1,1),以及求出圆C关于直线l对称的对称点,求出圆的半径即可求圆D的方程.
解答:
解:(1)圆C:x2+y2+4x+4y+m=0即 (x+2)2+(y+2)2=8-m
圆心C(-2,-2)到直线l的距离d=
=
,…(2分)
若圆C与直线l相离,则d>r,
∴r2=8-m<2即 m>6…(4分)
又r2=8-m>0即 m<8,
∴6<m<8…(6分)
(2)设圆D的圆心D的坐标为(x0,y0),由于圆C的圆心C(-2,-2),
依题意知:点D和点C关于直线l对称,…(7分)
则有:
⇒
,…(10分)
∴圆C的方程为:x2+y2=r2,又因为圆C过点P(1,1),
∴12+12=r2⇒r=
,
∴圆D的方程为:x2+y2=2…(12分)
圆心C(-2,-2)到直线l的距离d=
| |-2-2+2| | ||
|
| 2 |
若圆C与直线l相离,则d>r,
∴r2=8-m<2即 m>6…(4分)
又r2=8-m>0即 m<8,
∴6<m<8…(6分)
(2)设圆D的圆心D的坐标为(x0,y0),由于圆C的圆心C(-2,-2),
依题意知:点D和点C关于直线l对称,…(7分)
则有:
|
|
∴圆C的方程为:x2+y2=r2,又因为圆C过点P(1,1),
∴12+12=r2⇒r=
| 2 |
∴圆D的方程为:x2+y2=2…(12分)
点评:本题考查圆的方程的求法,点到直线的距离以及直线与的位置关系的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数f(x)的定义域为R,对任意x∈R有f(x)=f(x+6),且f(x)在(0,3)内单调递减,f(x)的图象关于直线x=3对称,则下列正确的结论是( )
| A、f(1.5)<f(3.5)<f(6.5) |
| B、f(6.5)<f(3.5)<f(1.5) |
| C、f(3.5)<f(1.5)<f(6.5) |
| D、f(3.5)<f(6.5)<f(1.5) |
i是虚数单位,复数
=( )
| 2i | ||
|
A、
| ||||||
B、
| ||||||
C、1-
| ||||||
D、1+
|
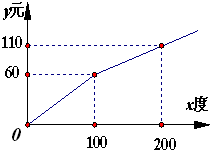 某地的水电资源丰富,并且得到了较好的开发,电力充足.某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的关系如图所示.
某地的水电资源丰富,并且得到了较好的开发,电力充足.某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的关系如图所示.