题目内容
17.将函数$f(x)=sin({2x-\frac{π}{6}})$的图象向右平移$\frac{π}{12}$个单位后得到的图象的一条对称轴是( )| A. | $x=\frac{π}{4}$ | B. | $x=\frac{3π}{8}$ | C. | $x=\frac{5π}{12}$ | D. | $x=\frac{7π}{24}$ |
分析 求出平移变换后的函数的解析式,然后判断函数的对称轴即可
解答 解:将函数$f(x)=sin({2x-\frac{π}{6}})$的图象向右平移$\frac{π}{12}$个单位长度得到函数g(x)=sin[2(x-$\frac{π}{12}$)$-\frac{π}{6}$]=sin(2x-$\frac{π}{3}$)的图象,
当2x-$\frac{π}{3}$=kπ$+\frac{π}{2}$时,函数g(x)取得最值,
所以x=$\frac{kπ}{2}+\frac{5π}{12}$,k∈Z是函数g(x)图象的对称轴.取k=0,得到图象的一条对称轴是x=$\frac{5π}{12}$;
故选:C.
点评 本题考查三角函数的图象的平移变换,函数的对称轴方程的判断,考查计算能力.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
8.命题“?x∈(0,1),x2-x<0”的否定是( )
| A. | ?x0∉(0,1),${x_0}^2-{x_0}≥0$ | B. | ?x0∈(0,1),${x_0}^2-{x_0}≥0$ | ||
| C. | ?x0∉(0,1),${x_0}^2-{x_0}<0$ | D. | ?x0∈(0,1),${x_0}^2-{x_0}≥0$ |
12.已知复数z满足z(1+i)=1-i,则z的共轭复数为( )
| A. | i | B. | 1+i | C. | 1-i | D. | -i |
9.天气预报说,在近期每天下雨的概率均为40%,用计算机随机函数产生0到9之间整数进行模拟,记产生的数为1,2,3,4时表示下雨,产生的数为5,6,7,8,9,0时表示不下雨,每次模拟产生3个数,20次模拟得到的实验数据如下:
则近3天中恰有2天下雨的概率估计为( )
| 907 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
| 431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
| A. | 0.2 | B. | 0.25 | C. | 0.35 | D. | 0.4 |
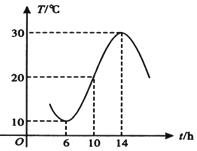 如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b(|ϕ|<π),则这段曲线的函数解析式可以为y=10sin($\frac{π}{8}x+\frac{3π}{4}$)+20;(6≤x≤14).
如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b(|ϕ|<π),则这段曲线的函数解析式可以为y=10sin($\frac{π}{8}x+\frac{3π}{4}$)+20;(6≤x≤14).