题目内容
7.设不等式组$\left\{\begin{array}{l}x+y-4≤0\\ x-y≥0\\ y≥0\end{array}\right.$表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是1$-\frac{π}{8}$.分析 画出图形,求出区域面积以及满足条件的P的区域面积,利用几何概型公式解答
解答 解:不等式组表示的区域D如图三角形区域,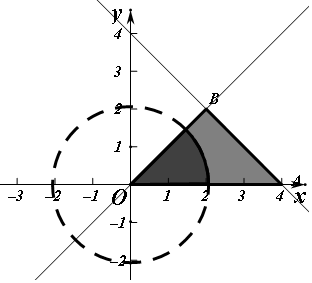 面积为$\frac{1}{2}×2\sqrt{2}×2\sqrt{2}=4$,
面积为$\frac{1}{2}×2\sqrt{2}×2\sqrt{2}=4$,
在区域D内随机取一个点P,则此点到坐标原点的距离大于2的点P落在圆x2+y2=4内对应区域外的部分,面积为$4-\frac{1}{8}π×4=4-\frac{π}{2}$,由几何概型的公式得到所求概率为:$\frac{4-\frac{π}{2}}{4}=1-\frac{π}{8}$;
故答案为:1-$\frac{π}{8}$
点评 本题给出不等式组表示的平面区域,求在区域内投点使该到原点距离大于2的概率,着重考查了二元一次不等式组表示的平面区域和几何概型等知识点.

练习册系列答案
相关题目
17.点M为直线5x+12y=0上任一点,F1(-13,0),F2(13,0),则下列结论正确的是( )
| A. | ||MF1|-|MF2||>24 | B. | ||MF1|-|MF2||=24 | C. | ||MF1|-|MF2||<24 | D. | 以上都有可能 |
12.设函数f(x)=min{xlnx,$\frac{{x}^{2}}{{e}^{x}}$}(min{a,b}表示a,b中的较小者),则函数f(x)的最大值为( )
| A. | $\frac{4}{{e}^{2}}$ | B. | 2ln2 | C. | $\frac{1}{e}$ | D. | $\frac{3}{2}$ln2 |
19.(1+2x)3(2-x)4的展开式中x的系数是( )
| A. | 96 | B. | 64 | C. | 32 | D. | 16 |
17.将函数$f(x)=sin({2x-\frac{π}{6}})$的图象向右平移$\frac{π}{12}$个单位后得到的图象的一条对称轴是( )
| A. | $x=\frac{π}{4}$ | B. | $x=\frac{3π}{8}$ | C. | $x=\frac{5π}{12}$ | D. | $x=\frac{7π}{24}$ |