题目内容
12.已知复数z满足z(1+i)=1-i,则z的共轭复数为( )| A. | i | B. | 1+i | C. | 1-i | D. | -i |
分析 由条件求出z,可得复数z的共轭复数.
解答 解:∵z(1+i)=1-i,
∴z=$\frac{1-i}{1+i}$=$\frac{(1-i)^{2}}{(1+i)(1-i)}$=-i,
∴z的共轭复数为i,
故选:A
点评 本题主要考查复数的基本概念,两个复数代数形式的乘除法法则的应用,虚数单位i的幂运算性质,属于基础题.

练习册系列答案
相关题目
7.复数z满足z(2+i)=1+3i,则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.将函数$f(x)=sin({2x-\frac{π}{6}})$的图象向右平移$\frac{π}{12}$个单位后得到的图象的一条对称轴是( )
| A. | $x=\frac{π}{4}$ | B. | $x=\frac{3π}{8}$ | C. | $x=\frac{5π}{12}$ | D. | $x=\frac{7π}{24}$ |
4.已知函数f(x)=x2+|ax+1|,命题p:?a∈R,f(x)为偶函数,则¬p为( )
| A. | ?a∈R,f(x)为奇函数 | B. | ?a∈R,f(x)为奇函数 | ||
| C. | ?a∈R,f(x)不为偶函数 | D. | ?a∈R,f(x)不为偶函数 |
2.已知长方体切去一个角的几何体直观图如图1所示给出下列4个平面图如图2:
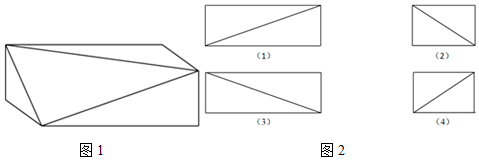
则该几何体的主视图、俯视图、左视图的序号依次是( )

则该几何体的主视图、俯视图、左视图的序号依次是( )
| A. | (1)(3)(4) | B. | (2)(4)(3) | C. | (1)(3)(2) | D. | (2)(4)(1) |