题目内容
6.函数f(x)=$\frac{x}{5π}$-sin(2x+$\frac{π}{6}$)的零点的个数为( )| A. | 16 | B. | 18 | C. | 19 | D. | 20 |
分析 作出y=$\frac{x}{5π}$和y=sin2x的函数图象,根据交点个数得出答案.
解答 解:∵y=sin2x的图象是由y=sin(2x+$\frac{π}{6}$)的图象左右平移得到的,
∴y=sin(2x+$\frac{π}{6}$)与y=$\frac{x}{5π}$的交点个数等于y=sin2x与y=$\frac{x}{5π}$的交点个数.
作出y=$\frac{x}{5π}$和y=sin2x在(0,+∞)上的函数图象,如图所示: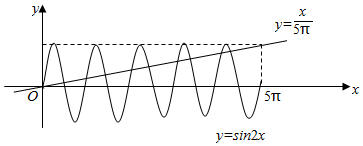
由图象可知y=$\frac{x}{5π}$和y=sin2x在(0,+∞)上有9个交点,
又y=$\frac{x}{5π}$和y=sin2x都是奇函数,
∴y=$\frac{x}{5π}$和y=sin2x在(-∞,0)上有9个零点,
又两函数都经过原点(0,0),
∴y=$\frac{x}{5π}$和y=sin2x有19个零点,
故选C.
点评 本题考查了函数零点与函数图象的关系,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.设对于任意实数x,不等式|x+7|≥m-1恒成立,且m的最大值为p.
(Ⅰ)求p的值;
(Ⅱ)若a,b,c∈R,且a+b+c=p,求证:${a^2}+{b^2}+{c^2}≥\frac{1}{3}$.
(Ⅰ)求p的值;
(Ⅱ)若a,b,c∈R,且a+b+c=p,求证:${a^2}+{b^2}+{c^2}≥\frac{1}{3}$.
17.已知三棱锥S-ABC,满足SA,SB,SC两两垂直,且SA=SB=SC=2,Q是三棱锥S-ABC外接球上一动点,则点Q到平面ABC的距离的最大值为( )
| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{2}}{4}$ |
1.一个不透明的袋子中装有除颜色外都相同的4个球,其中1个白球,1个红球,2个黄球,从中随机一次取出2个球,则这2个球恰有1个黄球的概率为( )
| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
18.在△ABC中,若a=1,A=60°,B=45°,则b=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
15.设函数f(x)=$\frac{2}{x}$+ln x,则f(x)的极小值为( )
| A. | 1 | B. | 2 | C. | 1+ln2 | D. | 2+ln2 |
3.已知数列{an}为等比数列,若a7=$\frac{5}{2}$,公比q=2${\;}^{\frac{1}{5}}$,则a3(a1+2a11+a21)的值为( )
| A. | 36 | B. | 6 | C. | $\frac{625}{16}$ | D. | $\frac{25}{4}$ |