题目内容
函数f（x）=ax+b的图象如图所示，其中a，b为常数，则下列结论正确的是（ ）
| A、a＞1，b＜0 |
| B、a＞1，b＞0 |
| C、0＜a＜1，b＞0 |
| D、0＜a＜1，b＜0 |
考点：指数函数的图像与性质
专题：计算题,函数的性质及应用
分析：由单调性可知a＞1，由图象变换可知b＜0．
解答：
解：由题意，函数f（x）=ax+b的图象可看成f（x）=ax向右平移得到，
故a＞1，b＜0；
故选A．
故a＞1，b＜0；
故选A．
点评：本题考查了指数函数的单调性及函数图象变换，属于基础题．
练习册系列答案
相关题目
点P为椭圆
+
=1上一点，以点P以及焦点F1、F2为顶点的三角形的面积为1，则P点的坐标为（ ）
| x2 |
| 5 |
| y2 |
| 4 |
A、（±
| ||||
B、（
| ||||
C、（
| ||||
D、（±
|
已知A，B在抛物线y2=2px（p＞0）上，O为坐标原点，如果|OA|=|OB|且△AOB的重心恰好是此抛物线的焦点F，则AB直线的方程是（ ）
| A、x-p=0 |
| B、4x-3p=0 |
| C、2x-5p=0 |
| D、2x-5p=0 |
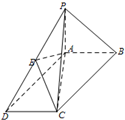如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．