题目内容
在平面直角坐标系xOy中,O为坐标原点,圆O过点M(1,
).
(1)求圆O的方程;
(2)若直线l1:y=mx-8与圆O相切,求m的值;
(3)过点(0,3)的直线l2与圆O交于A、B两点,点P在圆O上,若四边形OAPB是菱形,求直线l2的方程.
| 3 |
(1)求圆O的方程;
(2)若直线l1:y=mx-8与圆O相切,求m的值;
(3)过点(0,3)的直线l2与圆O交于A、B两点,点P在圆O上,若四边形OAPB是菱形,求直线l2的方程.
考点:直线与圆的位置关系
专题:直线与圆
分析:(1)求出半径,即可求圆O的方程;
(2)根据直线和圆相切求出圆心到直线的距离d=r,即可求m的值;
(3)设出直线l2的方程,利用四边形OAPB是菱形,则对角线垂直的条件即可,求直线l2的方程.
(2)根据直线和圆相切求出圆心到直线的距离d=r,即可求m的值;
(3)设出直线l2的方程,利用四边形OAPB是菱形,则对角线垂直的条件即可,求直线l2的方程.
解答:
解:(1)圆的半径r=
=
=2,
则圆O的方程为x2+y2=4;
(2)若直线l1:y=mx-8与圆O相切,
则圆心到直线的距离d=2,
即d=
=
=2,
解得m=±
;
(3)由题意可设直线l2的方程为y=kx+3,
若四边形OAPB是菱形,
∴OP与AB垂直平分,
故圆心O都直线l2的距离为
|OP|=1,
即
=1,即k2=8,解得k=±2
,
∴直线l2的方程为y=±2
x+3.
1+(
|
| 4 |
则圆O的方程为x2+y2=4;
(2)若直线l1:y=mx-8与圆O相切,
则圆心到直线的距离d=2,
即d=
| |-8| | ||
|
| 8 | ||
|
解得m=±
| 15 |
(3)由题意可设直线l2的方程为y=kx+3,
若四边形OAPB是菱形,
∴OP与AB垂直平分,
故圆心O都直线l2的距离为
| 1 |
| 2 |
即
| |3| | ||
|
| 2 |
∴直线l2的方程为y=±2
| 2 |
点评:本题主要考查直线和圆的位置关系的应用,根据圆心到直线的距离和半径之间的关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=
的定义域为( )
|
| A、[0,1) |
| B、(0,1) |
| C、(-∞,0]∪(1,+∞) |
| D、(-∞,0)∪(1,+∞) |
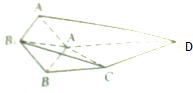 如图,ABCD为直角梯形,AB⊥AD,四边形ABB1A1是平行四边形,侧面ADA1⊥底面ABCD,AA1=
如图,ABCD为直角梯形,AB⊥AD,四边形ABB1A1是平行四边形,侧面ADA1⊥底面ABCD,AA1=