题目内容
在棱长为1的正方体ABCD-A1B1C1D1中,求:
(1)三棱锥C1-A1B1B的体积;
(2)异面直线A1B与AC所成的角.
(1)三棱锥C1-A1B1B的体积;
(2)异面直线A1B与AC所成的角.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)求三棱锥C1-A1B1B的体积.求出高与底面面积,即可.
(2)作出异面直线所成角,然后求解即可.
(2)作出异面直线所成角,然后求解即可.
解答:
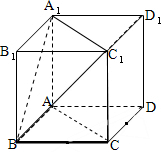 解:在棱长为1的正方体ABCD-A1B1C1D1中,
解:在棱长为1的正方体ABCD-A1B1C1D1中,
(1)三棱锥C1-A1B1B,转化为B-C1A1B1,三棱锥的高为BB1,底面是等腰直角三角形,所以所求三棱锥的条件为:
×
×1×1×1=
.
(2)∵AC∥A1C1,∴异面直线A1B与AC所成的角,就是∠BA1C1,△BA1C1是正三角形,∴∠BA1C1=60°.
异面直线A1B与AC所成的角为60°.
 解:在棱长为1的正方体ABCD-A1B1C1D1中,
解:在棱长为1的正方体ABCD-A1B1C1D1中,(1)三棱锥C1-A1B1B,转化为B-C1A1B1,三棱锥的高为BB1,底面是等腰直角三角形,所以所求三棱锥的条件为:
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
(2)∵AC∥A1C1,∴异面直线A1B与AC所成的角,就是∠BA1C1,△BA1C1是正三角形,∴∠BA1C1=60°.
异面直线A1B与AC所成的角为60°.
点评:本题是基础题,考查几何体的体积等知识,考查化归与转化的数学思想方法,以及空间想象能力、运算求解能力.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
设Sn是等比数列{an}的前n项和,且32a2+a7=0,则
=( )
| S5 |
| S2 |
| A、11 | B、5 | C、-8 | D、-11 |
将一根长为3米的绳子拉直后在任意位置剪断,分为两段,那么这两段绳子的长都不小于1米的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
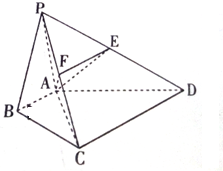 在四棱锥P-ABCD中,∠ABC=
在四棱锥P-ABCD中,∠ABC= 已知A,B两点分别在射线CM,CN(不含端点C)上运动,∠MCN=
已知A,B两点分别在射线CM,CN(不含端点C)上运动,∠MCN=