题目内容
18.已知函数f(x)=$\left\{{\begin{array}{l}{|{{{log}_2}x}|,\;0<x≤4}\\{{x^2}-12x+34\;,x>4}\end{array}}$,若方程f(x)=t,(t∈R)有四个不同的实数根x1,x2,x3,x4,则x1x2x3x4的取值范围为(32,34).分析 作函数f(x)=$\left\{{\begin{array}{l}{|{{{log}_2}x}|,\;0<x≤4}\\{{x^2}-12x+34\;,x>4}\end{array}}$的图象,从而可得x1x2=1,且x3+x4=12,(4<x3<6-$\sqrt{2}$),从而解得.
解答 解:作函数f(x)=$\left\{{\begin{array}{l}{|{{{log}_2}x}|,\;0<x≤4}\\{{x^2}-12x+34\;,x>4}\end{array}}$的图象如下,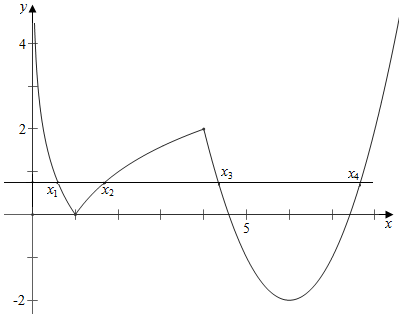 ,
,
结合图象可知,-log2x1=log2x2,
故x1x2=1,
令x2-12x+34=0得,x=6±$\sqrt{2}$,
令x2-12x+34=2得,x=6±2;
故x3+x4=12,(4<x3<6-$\sqrt{2}$),
故x1x2x3x4=x3x4
=x3(12-x3)
=-(x3-6)2+36,
∵4<x3<6-$\sqrt{2}$,
∴-2<x3-6<-$\sqrt{2}$,
∴32<-(x3-6)2+36<34,
故答案为:(32,34).
点评 本题考查了数形结合的思想应用及学生的作图能力,同时考查了配方法的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.下列说法错误的是( )
| A. | 命题p:“?x0∈R,x02+x0+1<0”,则¬p:“?x∈R,x2+x+1≥0” | |
| B. | 命题“若x2-4x+3=0,则x=3”的逆否命题是假命题 | |
| C. | 命题“若m>0,则方程x2+x-m=0有实数根”的否定是“若m>0,则方程x2+x-m=0没有实数根” | |
| D. | 若p∧q为假命题,则p∨q为假命题 |
6.已知复数$z=-1+\sqrt{3}i$,则$\frac{1}{z}$=( )
| A. | $-\frac{1}{4}-\frac{{\sqrt{3}}}{4}i$ | B. | $-\frac{1}{4}+\frac{{\sqrt{3}}}{4}i$ | C. | $\frac{1}{4}-\frac{{\sqrt{3}}}{4}i$ | D. | $\frac{1}{4}+\frac{{\sqrt{3}}}{4}i$ |
13.下列说法错误的是( )
| A. | 与众数、中位数相比,平均数可以反映出更多的关于样本数据全体的信息 | |
| B. | 标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小 | |
| C. | 人体的脂肪含量y与年龄x满足回归方程$\widehat{y}$=0.577x-0.448,当x=37时,$\widehat{y}$=0.209,这表明某人37岁时,其体内的脂肪含量一定是20.9% | |
| D. | 在样本数据较少时,用茎叶图表示数据不但可以保留数据的全部信息,而且可以随时记录 |
3.已知函数y=f(x)的图象是由y=sin2x向右平移$\frac{π}{12}$得到,则下列结论正确的是( )
| A. | f(0)<f(2)<f(4) | B. | f(2)<f(0)<f(4) | C. | f(0)<f(4)<f(2) | D. | f(4)<f(2)<f(0) |
8.抛物线y=$\frac{1}{2}$x2被直线y=x+4截得的线段的长度是( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{6}$ | C. | $\sqrt{6}$ | D. | 6$\sqrt{2}$ |