题目内容
14．已知集合A={x||x|＞2}，B={x|x2-3x＜0}，则A∪B=（ ）| A． | （-∞，-2）∪（0，+∞） | B． | （-∞，0）∪（2，+∞） | C． | （2，3） | D． | （-2，3） |
分析 先分别求出集合A和B，由此能求出A∪B．
解答 解：∵集合A={x||x|＞2}={x|x＞2或x＜-2}，
B={x|x2-3x＜0}={x|0＜x＜3}，
∴A∪B={x|x＜-2或x＞0}=（-∞，-2）∪（0，+∞）．
故选：A．
点评 本题考查并集的求法，是基础题，解题时要认真审题，注意并集性质的合理运用．
练习册系列答案
相关题目
5．若等比数列{an}的前n项和Sn满足Sn=a-（$\frac{1}{2}$）n-1，则直线（a-1）x-y+3=0与圆（x-a）2+y2=12的位置关系为（ ）
| A． | 相离 | B． | 相切 | C． | 相交 | D． | 无法确定 |
2．函数f（x）在定义域（0，+∞）内恒满足：①f（x）＞0；②2f（x）＜xf′（x）＜3f（x），其中f′（x）为f（x）的导函数，则（ ）
| A． | $\frac{1}{4}$＜$\frac{f（1）}{f（2）}$＜$\frac{1}{2}$ | B． | $\frac{1}{16}$＜$\frac{f（1）}{f（2）}$＜$\frac{1}{8}$ | C． | $\frac{1}{3}$＜$\frac{f（1）}{f（2）}$＜$\frac{1}{2}$ | D． | $\frac{1}{8}$＜$\frac{f（1）}{f（2）}$＜$\frac{1}{4}$ |
9．已知三棱锥S-ABC，其三视图中的正（主）视图和侧（左）视图如图所示，则该三棱锥的体积为（ ）
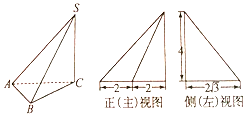
| A． | $\frac{{8\sqrt{3}}}{3}$ | B． | $\frac{{16\sqrt{3}}}{3}$ | C． | $\frac{{32\sqrt{3}}}{3}$ | D． | $16\sqrt{3}$ |
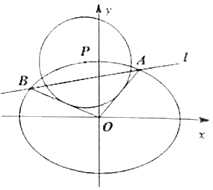如图，已知椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$e=\frac{{\sqrt{3}}}{2}$，P为椭圆E上的动点，P到点M（0，2）的距离的最大值为$\frac{2}{3}\sqrt{21}$，直线l交椭圆于A（x1，y1）、B（x2，y2）两点．
3．已知集合A={x|log2（x+1）＞0}，B={x|0＜x＜1}，则∁AB=（ ）
| A． | （0，1） | B． | （0，1] | C． | （1，+∞） | D． | [1，+∞） |
4．数列-1，3，-5，7，-9，…的一个通项公式为（ ）
| A． | an=2n-1 | B． | an=（-1）n（1-2n） | C． | an=（-1）n（2n-1） | D． | an（-1）n+1（2n-1） |