题目内容
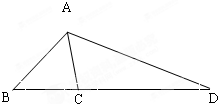
已知平面α∥平面β∥平面γ，两条直线l，m分别与平面α、β、γ相交于A、B、C和D、E、F，求证：
=
．
| AB |
| BC |
| DE |
| EF |
考点：平面与平面平行的性质
专题：空间位置关系与距离
分析：将α，β，γ从上到下放置，连结CD，交β于P，即l在m与之间作直线CD，从而利用两平行平面的性质定理得线线平面，再由平行直线分线段成比例定理得证．
解答：
证明：不妨设三个平面从上到下，依次为α，β，γ，
连结CD，交平面β于点P，连结AD，BP，PE，CF，如右图所示．
∵l∩CD=C，∴l与CD确定一个平面，设为α1，
∵α∩α1=AD，β∩α1=BP，且α∥β，
∴AD∥BP，∴
=
．
同理可证PE∥CF，∴
=
，
∴
=
．
连结CD，交平面β于点P，连结AD，BP，PE，CF，如右图所示．
∵l∩CD=C，∴l与CD确定一个平面，设为α1，
∵α∩α1=AD，β∩α1=BP，且α∥β，
∴AD∥BP，∴
| AB |
| BC |
| DP |
| PC |
同理可证PE∥CF，∴
| DP |
| PC |
| DE |
| EF |
∴
| AB |
| BC |
| DE |
| EF |
点评：本题考查了面面平行的性质定理的应用，值得注意的是：
1．题设中的直线m与l不一定共面，故通过直线CD凑成了定理中的“第三个平面”及“两条交线”．
2．连结l与m的直线除了选CD外，还可以是AF，或者其他直线；从上到下，当α，β，γ的顺序不同时，证法类似．
1．题设中的直线m与l不一定共面，故通过直线CD凑成了定理中的“第三个平面”及“两条交线”．
2．连结l与m的直线除了选CD外，还可以是AF，或者其他直线；从上到下，当α，β，γ的顺序不同时，证法类似．
练习册系列答案
互动英语系列答案
相关题目
函数f（x）=log
(x2-3x+2)的递减区间为（ ）
| 1 |
| 2 |
A、(-∞，
| ||
| B、（1，2） | ||
C、(
| ||
| D、（2，+∞） |
关于直线l，m与平面α，β的命题中，一定正确的是（ ）
| A、若l∥m，m?α，则l∥α |
| B、若l⊥β，α⊥β，则l∥α |
| C、若l⊥β，α∥β，则l⊥α |
| D、若l?β，α⊥β，则l⊥α |
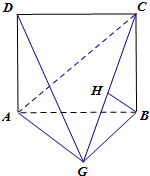已知四棱锥G-ABCD，四边形ABCD是长为2a的正方形，DA⊥平面ABG，且GA=GB，BH⊥平面CAG，垂足为H，且H在直线CG上．