题目内容
已知过原点的直线与函数y=|sin x|(x≥0)的图象有且只有三个交点,α是交点中横坐标的最大值,则 的值为 .
的值为 .
1
解析:y=|sin x|(x≥0)的图象如图,若过原点的直线与函数y=|sin x|(x≥0)的图象有且只有三个交点,
则第三个交点的横坐标为α,
且α∈( ,
, ),
),
又在区间(π,2π)上,y=|sin x|=-sin x,
则切点坐标为(α,-sin α),
又切线斜率为-cos α,
则切线方程为y+sin α=-cos α(x-α),

即y=(-cos α)x+αcos α-sin α.
又直线过原点,把(0,0)代入上式得,α=tan α,
∴ =
=
=(1+tan2α)cos2α
=(1+ )cos2α
)cos2α
=cos2α+sin2α
=1.

练习册系列答案
相关题目
 ,则tan(π+α)的值是( )
,则tan(π+α)的值是( ) (B)
(B)
 )在[0,
)在[0,

 ,
,

 ,k∈Z}.
,k∈Z}. )的图象向右平移
)的图象向右平移 个单位得到y=3sin2x的图象.
个单位得到y=3sin2x的图象. )在(0,π)上是减函数.
)在(0,π)上是减函数. ,π),sin α=
,π),sin α=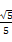 .
. +α)的值;
+α)的值; -2α)的值.
-2α)的值.